Câu hỏi:
22/07/2024 230Cho △ABC có AB>AC. Kẻ BN là tia phân giác của góc B (N∈AC). Kẻ CM là tia phân giác của góc C (M∈AB), CM và BN cắt nhau tại I. So sánh IC và IB?
A. IB < IC
B. IC > IB
C. IB = IC
D. IB > IC
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: D
Giải thích:
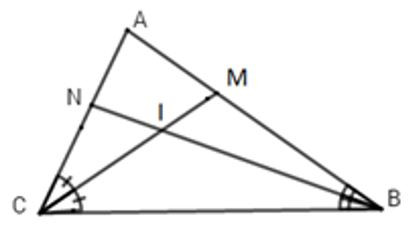
Vì AB>AC⇒^ACB>^ABC (1) (quan hệ giữa cạnh và góc đối diện trong tam giác)
Vì BN là tia phân giác của ^ABC⇒^NBC=^ABC2 (2) (tính chất phân giác)
Vì CM là tia phân giác của ^ACB⇒^MCB=^ACB2 (3) (tính chất phân giác)
Từ (1),(2),(3) ⇒^MCB>^NBC hay ^ICB>^IBC
Xét △BIC có ^MCB>^NBC (cmt) ⇒IB>IC ( quan hệ giữa góc và cạnh đối diện trong tam giác)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho △ABC có AB<AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD. So sánh ^CAD và ^CDA
Câu 3:
Cho tam giác ABC có ˆB=70°, . Em hãy chọn câu trả lời đúng nhất:
Câu 4:
Cho tam giác ABC vuông tại A. Trên hai cạnh góc vuông AB, AC lấy lần lượt hai điểm M và N. So sánh MN và BC
Câu 7:
Cho có . Trên AB lấy điểm P, trên AC lấy điểm N sao cho . So sánh và
Câu 10:
Cho tam giác ABC vuông tại A. Vẽ phân giác BD. So sánh AB và AD, AD và DC
Câu 12:
Cho tam giác ABC có ( là các góc nhọn). Vẽ phân giác AD. So sanh BD và CD


