Nội dung bài viết

    Xem thêm

    Bằng phương pháp quy nạp, chứng minh: n^5 – n chia hết cho 5 với mọi n thuộc ℕ*

    Lời giải Bài 9 trang 38 sách Chuyên đề Toán lớp 10 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập.

    1 440 10/11/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Chuyên đề Toán 10 Cánh diều Bài 2: Nhị thức newton

    Bài 9 trang 38 Chuyên đề Toán 10:

    Bằng phương pháp quy nạp, chứng minh:

    a) n5 – n chia hết cho 5 ∀ n ∈ ℕ*;

    b) n7 – n chia hết cho 7 ∀ n ∈ ℕ*.

    Lời giải:

    a)

    +) Với n = 1, ta có: 15 – 1 = 0 ⁝ 5.

    Vậy mệnh đề đúng với n = 1.

    +) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: (k + 1)5 – (k + 1) ⁝ 5.

    Thật vậy, theo giả thiết quy nạp ta có: k5 – k ⁝ 5.

    Khi đó:

    (k + 1)5 – (k + 1)

    =k5+5k4+10k3+10k2+5k+1−k+1

    =k5−k+5k4+10k3+10k2+5k

    Mà k5−k và 5k4+10k3+10k2+5k đều chia hết cho 5, do đó

    k5−k+5k4+10k3+10k2+5k ⁝ 5 hay (k + 1)5 – (k + 1) ⁝ 5.

    Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*.

    b)

    +) Với n = 1, ta có: 17 – 1 = 0 ⁝ 7.

    Vậy mệnh đề đúng với n = 1.

    +) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: (k + 1)7 – (k + 1) ⁝ 7.

    Thật vậy, theo giả thiết quy nạp ta có: k7 – k ⁝ 7.

    Khi đó:

    (k + 1)7 – (k + 1)

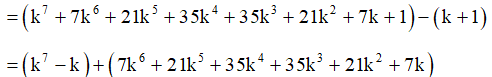
    Chuyên đề Toán 10 Bài 2: Nhị thức newton - Cánh diều (ảnh 1)

    Mà k7−k và 7k6+21k5+35k4+35k3+21k2+7k đều chia hết cho 7, do đó

    k7−k+7k6+21k5+35k4+35k3+21k2+7k ⁝ 7 hay (k + 1)7 – (k + 1) ⁝ 7.

    Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n ∈ ℕ*.

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Cánh diều hay, chi tiết khác:

    Hoạt động 1 trang 31 Chuyên đề Toán 10: a) Chọn số thích hợp cho ? trong khai triển biểu thức sau: Hoạt động 1 trang 31 Chuyên đề Toán 10...

    Luyện tập 1 trang 32 Chuyên đề Toán 10: Khai triển biểu thức (x + 2)7...

    Luyện tập 2 trang 32 Chuyên đề Toán 10: Cho n∈ℕ*. Chứng minh: Luyện tập 2 trang 32 Chuyên đề Toán 10...

    Hoạt động 2 trang 33 Chuyên đề Toán 10: Ta đã biết: Hoạt động 2 trang 33 Chuyên đề Toán 10...

    Luyện tập 3 trang 34 Chuyên đề Toán 10: Sử dụng tam giác Pascal để khai triển: a) (x + y)7...

    Hoạt động 3 trang 35 Chuyên đề Toán 10: Xét dãy các hệ số trong khai triển nhị thức (a + b)4 (Hình 7a)...

    Luyện tập 4 trang 35 Chuyên đề Toán 10: Tìm hệ số lớn nhất trong khai triển của: a) (a + b)2022...

    Hoạt động 4 trang 36 Chuyên đề Toán 10: Quan sát khai triển nhị thức: Hoạt động 4 trang 36 Chuyên đề Toán 10...

    Luyện tập 5 trang 36 Chuyên đề Toán 10: Xét khai triển của (x + 5)15. a) Nêu số hạng...

    Bài 1 trang 37 Chuyên đề Toán 10: Khai triển các biểu thức sau: a) (2x + y)6...

    Bài 2 trang 37 Chuyên đề Toán 10: Tính: Bài 2 trang 37 Chuyên đề Toán 10...

    Bài 3 trang 37 Chuyên đề Toán 10: Chứng minh: Bài 3 trang 37 Chuyên đề Toán 10...

    Bài 4 trang 37 Chuyên đề Toán 10: Xác định hệ số của: a) x12 trong khai triển của (x + 4)30...

    Bài 5 trang 37 Chuyên đề Toán 10: Xét khai triển của x+5212...

    Bài 6 trang 37 Chuyên đề Toán 10: Xét khai triển của x2+1521...

    Bài 7 trang 38 Chuyên đề Toán 10: Tìm hệ số lớn nhất trong khai triển của: a) (a + b)8...

    Bài 8 trang 38 Chuyên đề Toán 10: Chứng minh công thức nhị thức Newton bằng phương pháp quy nạp: Bài 8 trang 38 Chuyên đề Toán 10...

    Bài 10 trang 38 Chuyên đề Toán 10: Cho tập hợp A = {x1; x2; x3; ... ; xn} có n phần tử. Tính số tập hợp con của A...

    Bài 11 trang 38 Chuyên đề Toán 10: Một nhóm gồm 10 học sinh tham gia chiến dịch Mùa hè xanh...

    Bài 12 trang 38 Chuyên đề Toán 10: Để tham gia một cuộc thi làm bánh, bạn Tiến làm 12 chiếc bánh...

    Bài 13 trang 38 Chuyên đề Toán 10: Bác Thành muốn mua quà cho con nhân dịp sinh nhật nên đã đến một cửa hàng đồ chơi...

    Bài 14 trang 38 Chuyên đề Toán 10: Giả sử tính trạng ở một loài cây được quy định do tác động cộng gộp của n cặp alen...

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Cánh diều hay, chi tiết khác:

    Bài 1: Phương pháp quy nạp toán học

    Bài 1: Elip

    Bài 2: Hypebol

    Bài 3: Parabol

    Bài 4: Ba đường conic

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 440 10/11/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: