Nội dung bài viết

    Xem thêm

    Nêu điều kiện để x là căn bậc hai số học của số a không âm

    Với giải câu hỏi 1 trang 39 sgk Toán lớp 9 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 747 07/12/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Ôn tập chương 1

    Video Giải Câu hỏi 1 trang 39 Toán lớp 9 tập 1

    Câu hỏi 1 trang 39 Toán lớp 9 tập 1: Nêu điều kiện để x là căn bậc hai số học của số a không âm. Cho ví dụ

    *Lời giải

    Để x là căn bậc hai số học của số a không âm là x ≥ 0 và x2 = a.

    Ví dụ 2 là căn bậc hai số học của 4 vì 2 > 0 và 22 = 4.

    *Phương pháp giải

    Áp dụng tính chất căn bậc hai

    *Lý thuyết và các dạng bài toán về căn bậc hai số học:

    Giới thiệu bảng căn bậc hai

    + Bảng được chia thành các hàng và các cột.

    + Căn bậc hai của các số được viết bởi không qua ba chữ số từ 1,00 đến 99,9 được ghi sẵn trong bảng ở các cột từ cột 0 đến cột 9.

    + Tiếp đó là chín cột hiệu chính được dùng để hiệu chính chữ số cuối của căn bậc hai của các số được viết bởi bốn chữ số từ 1,000 đến 99,99.

    + Bảng căn bậc hai.

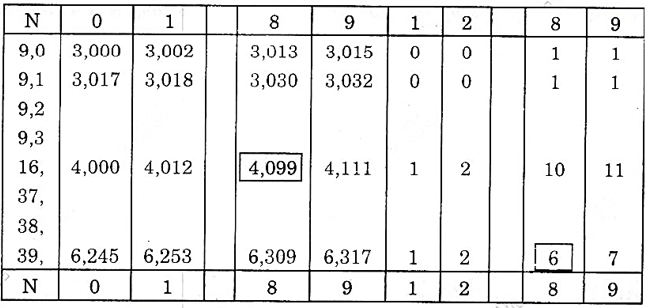
    Lý thuyết Bảng căn bậc hai chi tiết – Toán lớp 9 (ảnh 1)

    Tìm căn bậc hai của số không âm và nhỏ hơn 1

    Chú ý. Để thực hành nhanh, khi tìm căn bậc hai của số không âm lớn hơn 100 hoặc nhỏ hơn 1, ta dùng hướng dẫn của bảng: “Khi dời dấu phẩy trong số N đi 2, 4, 6, …chữ số thì dời dấu phẩy trong số N đi 1, 2, 3, …chữ số”.

    Đưa một thừa số ra ngoài dấu căn

    • Với a ≥ 0, b ≥ 0, ta có: a2b=ab. Phép biến đổi này được gọi là phép đưa thừa số ra ngoài dấu căn.

    • Đôi khi, ta phải biến đổi biểu thức dưới dấu căn về dạng thích hợp rồi mới thực hiện được phép đưa thừa số ra ngoài dấu căn.

    • Có thể sử dụng phép đưa thừa số ra ngoài dấu căn để rút gọn biểu thức chứa căn thức bậc hai.

    Tổng quát: Với hai biểu thức A, B mà B ≥ 0 ta có A2 . B=  |A|B, tức là:

    Nếu A ≥ 0 và B ≥ 0 thì A2B=AB;

    Nếu A < 0 và B ≥ 0 thì A2B=−AB.

    Đưa thừa số vào trong dấu căn

    • Phép đưa thừa số ra ngoài dấu căn có phép biến đổi ngược với nó là phép đưa thừa số vào trong dấu căn.

    Với A ≥ 0 và B ≥ 0 thì AB=A2B.

    Với A < 0 và B ≥ 0 thì AB=− A2B.

    Xem thêm các bài viết liên quan hay, chi tiết:

    Lý thuyết Bảng căn bậc hai (mới 2024 + Bài Tập) – Toán 9

    Toán 9 Bài 7 (Kết nối tri thức): Căn bậc hai và căn thức bậc hai

    50 Bài tập Bảng căn bậc hai chọn lọc Toán 9 mới nhất

    Xem thêm lời giải bài tập Toán lớp 9 hay, chi tiết khác:

    Câu hỏi 2 trang 39 Toán 9 Tập 1: Chứng minh a2=a với mọi số a...

    Câu hỏi 3 trang 39 Toán 9 Tập 1: Biểu thức A phải thỏa mãn điều kiện gì...

    Câu hỏi 4 trang 39 Toán 9 Tập 1: Phát biểu và chứng minh định lí về mối liên hệ giữa phép nhân và phép khai phương...

    Câu hỏi 5 trang 39 Toán 9 Tập 1: Phát biểu và chứng minh định lí về mối liên hệ giữa phép chia và phép khai phương...

    Bài 70 trang 40 Toán 9 Tập 1: Tìm giá trị các biểu thức sau bằng cách biến đổi, rút gọn thích hợp...

    Bài 71 trang 40 Toán 9 Tập 1: Rút gọn các biểu thức sau...

    Bài 72 trang 40 Toán 9 Tập 1: Phân tích thành nhân tử (với các số x, y, a, b không âm và a ≥ b)...

    Bài 73 trang 40 Toán 9 Tập 1: Rút gọn rồi tính giá trị các biểu thức sau...

    Bài 74 trang 40 Toán 9 Tập 1: Tìm x, biết...

    Bài 75 trang 40 Toán 9 Tập 1: Chứng minh các đẳng thức sau...

    Bài 76 trang 41 Toán 9 Tập 1: Cho biểu thức ...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 747 07/12/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: