Dạng 3: Chứng minh các hệ thức hình học
-
582 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC và các đường chéo BD, AC lần lượt tại M, N, P, Q. Khi đó tỉ số bằng:
Xem đáp án
Đáp án đúng là: C
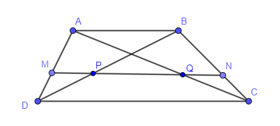
Xét tam giác ADB có MP // AB nên theo định lí Thalès ta có:
(1)
Xét tam giác CDB có NP // DC nên theo định lí Thalès ta có:
(2)
Từ (1) và (2) suy ra .
Câu 2:
23/07/2024Cho góc xAy khác góc bẹt. Trên tia Ax lấy các điểm B, C. Qua B và C kẻ hai đường thẳng song song với nhau, cắt Ay lần lượt tại D và E. Qua E vẽ đường thẳng song song với CD cắt tia Ax tại F. Khi đó AC2 bằng
Xem đáp án
Đáp án đúng là: A
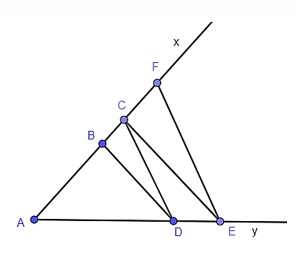
Xét tam giác ACE có CE // BD nên theo định lí Thalès ta có:
(1)
Xét tam giác AFE có FE // CD nên theo định lí Thalès ta có:
(2)
Từ (1) và (2) suy ra .
Từ đó ta có AC ⋅ AC = AB ⋅ AF hay AC2 = AB ⋅ AF.
Câu 3:
16/07/2024 Xem đáp án
Đáp án đúng là: C
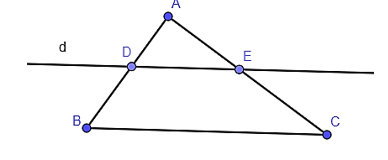
Trong tam giác ABC có nên DE // BC (định lí Thalès đảo).
Do đó theo định lí Thalès ta có , .
Vậy C sai.
Câu 4:
20/07/2024Cho tam giác ABC. Trên cạnh BC lấy điểm D sao cho BC = 2BD. Trên đoạn AD lấy điểm O sao cho . Gọi I là giao điểm của CO và AB. Tỉ số là:
Xem đáp án
Đáp án đúng là: C
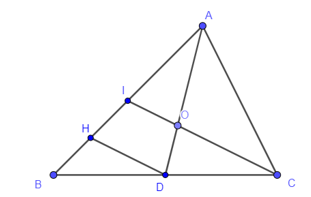
Kẻ DH // CI (H ∈ AB), do đó DH // IO.
Xét tam giác ADH có DH // IO nên theo định lí Thalès ta có:
hay .
Suy ra AI = 3t và IH = 2t (với t > 0).
Ta có D thuộc cạnh BC và BC = 2BD, suy ra BC = 2CD.
Xét tam giác BIC có DH // IC nên theo định lí Thalès ta có:
hay
Suy ra BI = 2IH = 2 ⋅ 2t = 4t.
Vậy .
Câu 5:
23/07/2024Cho tam giác ABC có trung tuyến AM và điểm E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC, cắt AB tại D và kẻ đường thẳng song song với AB, cắt AC tại F. Khi đó bằng tỉ số
Xem đáp án
Đáp án đúng là: D
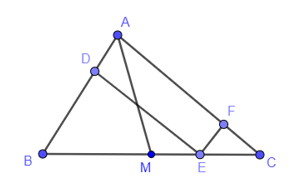
Xét tứ giác ADEF có:
AD // EF (D ∈ AB)
AF // DE (F ∈ AC)
Suy ra tứ giác ADEF là hình bình hành.
Do đó AF = DE (1).
Xét tam giác ABC có EF // AB nên theo định lí Thalès ta có:
(2)
Từ (1) và (2) suy ra .
Câu 6:
16/07/2024Cho tam giác ABC nhọn, M là trung điểm BC và H là trực tâm của tam giác ABC. Đường thẳng qua H và vuông góc với MH cắt AB và AC theo thứ tự ở I và K. Qua C kẻ đường thẳng song song với IK, cắt AH và AB theo thứ tự tại N và D. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: A
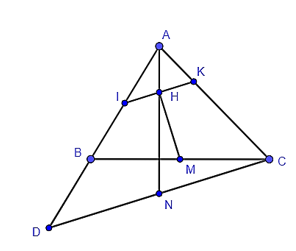
Ta có AN ⊥ BC (do H là trực tâm của tam giác ABC) nên HN ⊥ CM (H ∈ AN, M ∈ BC).
Theo đề bài ta có IK // DC, IK ⊥ HM, do đó HM ⊥ DC hay HM ⊥ NC (N ∈ DC).
Tam giác HNC có: HM ⊥ NC, CM ⊥ HN.
Do đó M là trực tâm của tam giác HNC.
Suy ra MN ⊥ HC.
Lại có HC ⊥ AB nên MN // AB hay MN // DB.
Xét tam giác CBD có MN // DB nên theo định lí Thalès ta có:
hay (Vì CM = MB, do M là trung điểm của BC)
Suy ra CN = ND.
Câu 7:
22/07/2024Cho hình bình hành ABCD. Gọi E là một điểm bất kì trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC tại F và kẻ đường thẳng song song với BD cắt AD tại H. Đường thẳng kẻ qua F song song với BD cắt CD tại G. Khi đó AH ⋅ CD bằng
Xem đáp án
Đáp án đúng là: B
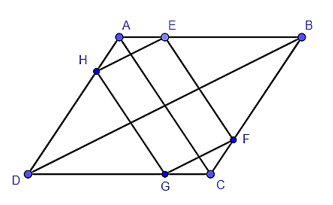
Xét tam giác ABD có HE // BD nên theo định lí Thalès ta có:
(1).
Xét tam giác CBD có GF // BD nên theo định lí Thalès ta có:
(2).
Xét tam giác ABC có EF // AC nên theo định lí Thalès ta có:
(3).
Từ (1), (2), (3) suy ra hay .
Từ đó suy ra AH ⋅ CD = AD ⋅ CG.
Câu 8:
18/07/2024Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm D, E, trên tia Oy lấy hai điểm F, G sao cho FD // EG. Đường thẳng kẻ qua G song song với EF cắt Ox tại H.
Tích OD ⋅ OH bằng
Xem đáp án
Đáp án đúng là: C
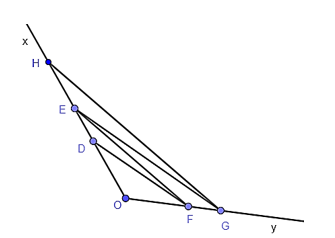
Xét tam giác OHG có EF // HG nên theo định lí Thalès ta có:
(1).
Xét tam giác OEG có DF // EG nên theo định lí Thalès ta có:
(2).
Từ (1) và (2) suy ra .
Từ đó ta có OE ⋅ OE = OH ⋅ OD hay OE2 = OH ⋅ OD.
Câu 9:
19/07/2024Cho tam giác ABC, từ điểm D trên cạnh AB kẻ đường thẳng song song với BC cắt AC tại E. Trên tia đối của tia CA, lấy điểm F sao cho CF = DB. Gọi M là giao điểm của DF và BC. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: B
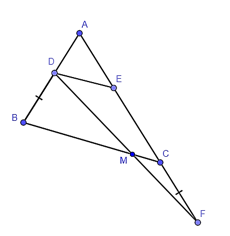
Xét tam giác ABC có DE // BC nên theo định lí Thalès ta có:
hay (1).
Xét tam giác DEF có DE // MC (M ∈ BC) nên theo định lí Thalès ta có:
(2).
Mà CF = DB (3).
Từ (1), (2) và (3) suy ra .
Câu 10:
20/07/2024Cho tam giác ABC có đường cao AH. Trên AH lấy các điểm K, I sao cho AK = KI = IH. Qua I, K lần lượt vẽ các đường thẳng EF // BC, MN // BC (E, M ∈ AB; F, N ∈ AC). Khi đó bằng
Xem đáp án
Đáp án đúng là: D
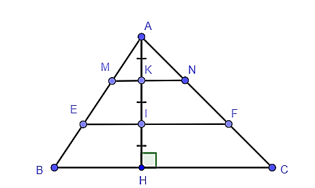
Vì MN // BC, EF // BC nên MN // BC // EF.
Trong tam giác ABH có EI // BH (I ∈ EF, H ∈ BC) nên theo định lí Thalès ta có:
hay .
Trong tam giác AIF có KN // IF (I ∈ EF, K ∈ MN) nên theo định lí Thalès ta có:
hay .
Ta có .