Dạng 2: Chứng minh đường thẳng song song
-
643 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Cho hình vẽ. Chọn khẳng định sai
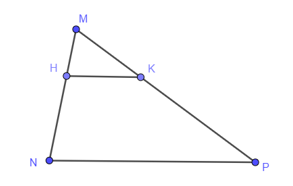
Xem đáp án
Đáp án đúng là: C
Theo định lí Thalès đảo nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Nên C sai.
Câu 2:
16/07/2024Cho hình vẽ. Chọn đáp án đúng trong các đáp án sau.
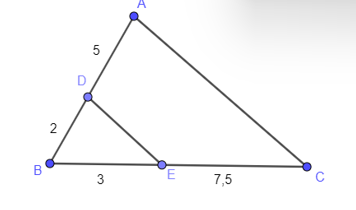
Xem đáp án
Đáp án đúng là: B
Trong tam giác ABC, ta có: .
Vì nên DE // AC (định lí Thalès đảo).
Câu 3:
19/07/2024Cho tam giác ABC có điểm M trên cạnh BC sao cho BC = 4CM. Trên cạnh AC lấy điểm N sao cho . Khẳng định nào sau đây là đúng khi nói về mối quan hệ giữa hai đường thẳng AB và MN.
Xem đáp án
Đáp án đúng là: A
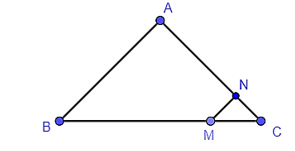
Theo tính chất của tỉ lệ thức ta có:
, do đó hay (1).
Vì BC = 4CM nên (2).
Từ (1) và (2) suy ra .
Trong tam giác ABC có nên MN // AB (định lí Thalès đảo).
Câu 4:
19/07/2024Cho hình vẽ dưới, khẳng định nào sau đây là đúng?
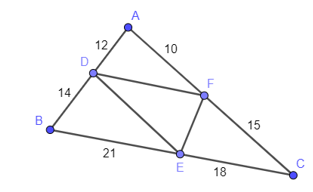
Xem đáp án
Đáp án đúng là: D
Ta có
Suy ra .
Trong tam giác ABC có nên DE // AC (định lí Thalès đảo).
Câu 5:
16/07/2024Cho tam giác ABC. Điểm O nằm trong tam giác. Lấy điểm D trên AO, từ D kẻ DE // AB (E ∈ OB) và DF // AC (F ∈ OC). Khẳng định nào sau đây là sai?
Xem đáp án
Đáp án đúng là: A
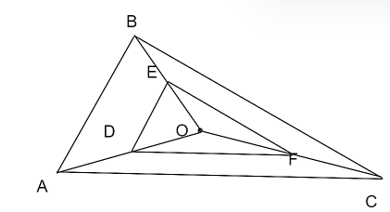
Xét tam giác OAB có DE // AB nên theo định lí Thalès ta có:
(1)
Xét tam giác OAC có DF // AC nên theo định lí Thalès ta có:
(2)
Từ (1) và (2) suy ra .
Trong tam giác OBC có nên EF // BC (định lí Thalès đảo).
Vậy A sai.
Câu 6:
20/07/2024Cho tứ giác MNPQ, gọi K, L lần lượt là trọng tâm của tam giác MNP và NPQ. Khi đó KL song song với đường thẳng nào dưới đây?
Xem đáp án
Đáp án đúng là: D
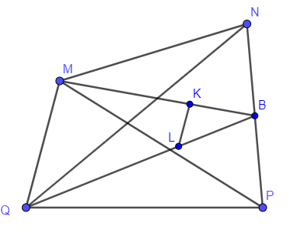
Gọi B là trung điểm của NP.
Vì K là trọng tâm tam giác MNP nên (tính chất trọng tâm của tam giác) hay (1).
Vì L là trọng tâm tam giác NPQ nên (tính chất trọng tâm của tam giác) hay (2).
Từ (1) và (2) suy ra .
Trong tam giác BMQ có nên MQ // KL (định lí Thaslès đảo).
Câu 7:
16/07/2024Cho tam giác ABC, I và K là hai điểm bất kì trên cạnh AB và AC. Từ I kẻ IM // BK (M ∈ AC), từ K kẻ KN // CI (N ∈ AB). Khi đó MN …… BC. Từ thích hợp điền vào chỗ chấm là:
Xem đáp án
Đáp án đúng là: B
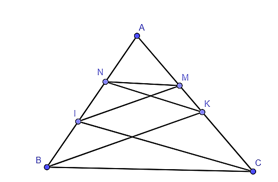
Xét tam giác ABK có IM // BK nên theo định lí Thalès ta có:
(1)
Xét tam giác AIC có IC // NK nên theo định lí Thalès ta có:
(2)
Nhân theo vế (1) với (2) ta được:
Suy ra .
Trong tam giác ABC có nên MN // BC (định lí Thalès đảo).
Câu 8:
21/07/2024Cho hình bên, biết AB = 9 cm, AC = 12 cm, IB = 6 cm, KC = 8 cm. Kết luận nào sau đây là đúng?
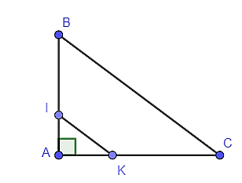
Xem đáp án
Đáp án đúng là: B
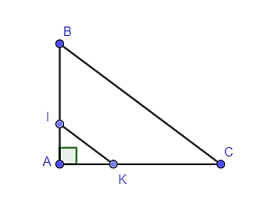
Ta có do đó .
Trong tam giác ABC có nên IK // BC (định lí Thaslès đảo).
Câu 9:
16/07/2024Cho tam giác ABC vuông tại A, đường cao AH. Từ điểm D nằm giữa H và C, vẽ DE ⊥ DC (E ∈ AC), DK ⊥ AC (K ∈ AC). Khi đó BE song song với
Xem đáp án
Đáp án đúng là: C
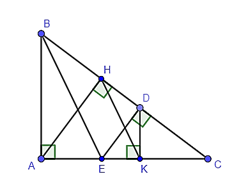
Có DE ⊥ DC nên DE ⊥ BC (D ∈ BC).
Vì AH ⊥ BC nên AH // DE.
Lại có DK ⊥ AC , AB ⊥ AC nên DK // AB.
Xét tam giác ABC có DK // AB nên theo định lí Thalès ta có:
(1)
Xét tam giác AHC có DE // AH nên theo định lí Thalès ta có:
(2)
Chia theo vế (1) cho (2) ta được:
Suy ra .
Trong tam giác CEB có nên HK // BE (định lí Thaslès đảo).
Câu 10:
23/07/2024Cho tam giác ABC nhọn, các đường cao AD, BE, CF đồng quy tại H. Gọi M, N, P, Q lần lượt là hình chiếu của D trên AB, BE, CF, AC. Khẳng định nào sau đây sai?
Xem đáp án
Đáp án đúng là: A
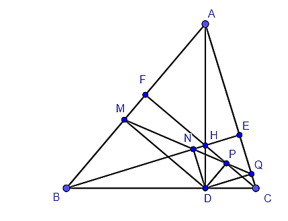
Ta có QD ⊥ AC, HE ⊥ AC (H ∈ BE) nên HE // QD hay BE // QD (H ∈ BE).
Xét tam giác ADQ có HE // DQ nên theo định lí Thalès ta có: (1).
Có HF ⊥ AB (H ∈ CF), DM ⊥ AB nên HF // DM hay CF // DM.
Xét tam giác AMD có HF // DM nên theo định lí Thalès ta có: (2).
Từ (1) và (2) suy ra .
Trong tam giác AMQ có nên EF // MQ (định lí Thaslès đảo) (*).
Xét tam giác BFC có CF // DM nên theo định lí Thalès ta có: (3).
Có DN ⊥ BE, BE ⊥ EC (E ∈ AC) nên DN // CE.
Xét tam giác BEC có DN // CE nên theo định lí Thalès ta có: (4).
Từ (3) và (4) suy ra .
Trong tam giác BEF có nên MN // EF (định lí Thaslès đảo) (**).
Xét tam giác BEC có QD // BE nên theo định lí Thalès ta có: (5).
Có DP ⊥ CF, BF ⊥ CF (F ∈ AB) nên DP // BF.
Xét tam giác BFC có DP // BF nên theo định lí Thalès ta có: (6).
Từ (5) và (6) suy ra .
Trong tam giác CEF có nên PQ // EF (định lí Thaslès đảo)(***)
Từ (*), (**), (***) suy ra M, N, P, Q thẳng hàng.
Vậy A sai.