Trắc nghiệm Ôn tập Toán 12 Chương 2 (có đáp án)
Trắc nghiệm Toán 12 Bài Ôn tập Chương 2
-
434 lượt thi
-
28 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
22/07/2024Hàm số có tập xác định là:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Điều kiện xác định của hàm số là:
Vậy tập xác định là:
Câu 3:
21/07/2024Đạo hàm của hàm số là:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Với
Áp dụng công thức
Câu 4:
21/07/2024Tìm tập nghiệm S của hệ phương trình
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải.
Điều kiện:
Hệ phương trình
Cách 2. Dùng CASIO thử từng đáp án.
Câu 5:
16/07/2024Tìm tất cả các cặp số log(2x+2y)=1
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
Điều kiện: .
Từ (1) và (2), ta có hệ
Câu 6:
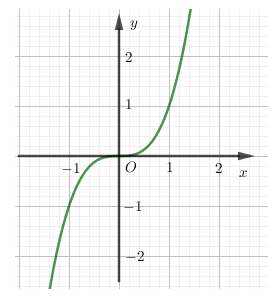
23/07/2024Hàm số nào trong hàm số sau đây có đồ thị phù hợp với hình vẽ bên?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Đồ thị của hình vẽ là đồ thị hàm bậc ba
Câu 8:
18/07/2024Cho a, b > 0. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có:
⇔blna=alnb
Câu 9:
13/07/2024Tính giá trị của biểu thức P=ln(tan10)+ln(tan20)+..+ln(tan890)
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:

Câu 10:
14/07/2024Cho hệ phương trình . Chọn khẳng định đúng?
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
Điều kiện: . Do đó A sai.
Xét phương trình thứ nhất của hệ: .
Đặt , phương trình trở thành
Phương tình thứ hai của hệ:
Từ đó ta có
thỏa mãn điều kiện.
Vậy hệ phương trình đã cho có một nghiệm duy nhất (x;y)=(−1;−2)
Câu 11:
20/07/2024Cho số thực x thỏa P=(log2x)2
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Điều kiện:
Đặt
Ta có:
⇒P=27
Câu 12:
23/07/2024Cho hệ phương trình . Chọn kết luận đúng:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Đặt thì hệ trở thành:
Do đó:
Câu 13:
23/07/2024Phương trình có tất cả bao nhiêu nghiệm thực?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
(1)
Phương trình có 3 nghiệm.
Câu 14:
18/07/2024Tập nghiệm của bất phương trình là:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
⇔−1≤x≤0∨x>1
Câu 15:
23/07/2024Giải phương trình 4x−6.2x+8=0
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Đặt
Phương trình đã cho trở thành
Với
Với
Vậy phương trình có hai nghiệm
Câu 16:
14/07/2024Cho a là số thực tùy ý và b, c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số G, A (1; - 1; - 2) và . Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
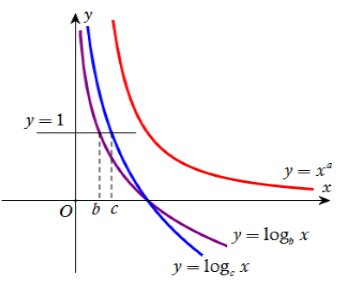
Nhận thấy hàm số . Do đó ta loại ngay đáp án C, D (vì b, c là các số thực dương khác 1)
Kẻ đường thẳng y = 1 cắt đồ thị của hai hàm số G, A (1; - 1; - 2) lần lượt tại điểm có hoành độ là x = b và x = c như hình vẽ. Dựa vào hình vẽ ta thấy
Vậy a<b<c
Câu 17:
18/07/2024Gọi . Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Điều kiện:
Hệ phương trình tương đương với:
Câu 18:
23/07/2024Tìm tập nghiệm của bất phương trình 7x≥10−3x
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Hàm số đồng biến trên R.
Hàm số nghịch biến trên R
Phương trình có nghiệm duy nhất x = 1 nên:
+ Nếu
+ Nếu hay bất phương trình không thỏa với x <1
Vậy bất phương trình đã cho có nghiệm [1;+∞)
Câu 19:
23/07/2024Cho được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Với ta có:
Mặt khác, dựa vào hình dáng đồ thị ta suy ra
Từ đó suy ra A là phương án đúng.
Câu 20:
22/07/2024Có bao nhiêu giá trị thực của tham số m để phương trình có đúng 3 nghiệm thực phân biệt.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Đặt
Khi đó phương trình trở thành:
Để phương trình có 3 nghiệm thì có một nghiệm duy nhất khác 1; 2 hoặc có hai nghiệm phân biệt, trong đó có một nghiệm bằng 1 hoặc 2, nghiệm còn lại khác 1 và 2.
TH1: (*) có nghiệm duy nhất x = 0.
Tức
TH2: (*) có một nghiệm x = 1 thì:
Khi đó phương trình (*) là thỏa mãn yêu cầu.
TH3: (*) có nghiệm x = 2.
Khi đó
Khi đó pt (*) là: thỏa mãn yêu cầu.
Vậy
Câu 21:
19/07/2024Tìm tất cả các giá trị thực của tham số m để phương trình sau có hai nghiệm thực phân biệt: (x+m−4)=0
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Yêu cầu bài toán
Dùng định lí về dấu tam thức bậc hai.
Để thỏa yêu cầu bài toán ta phải có phương trình
Câu 22:
23/07/2024Hỏi phương trình có tất cả bao nhiêu nghiệm thực?
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
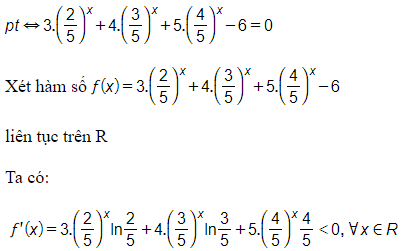
Do đó hàm số luôn nghịch biến trên R mà hay phương trình f (x) = 0 có nghiệm duy nhất thuộc (0; 2)
Câu 23:
14/07/2024Theo dự báo với mức tiêu thụ dầu không đổi như hiện nay thì trữ lượng dầu nước A sẽ hết sau 100 năm nữa. Nhưng do nhu cầu thực tế, mức tiêu thụ tăng lên 4% mỗi năm. Hỏi sau bao nhiêu năm số dầu dự trữ của nước A sẽ gần như hết (còn nhưng không đủ dùng cho năm tới)? Giả thiết nước này không nhập khẩu dầu từ nước khác.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Gọi A là trữ lượng dầu, x là lượng dầu sử dụng năm đầu tiên ta có A = 100x
Qua năm thứ hai trữ lượng dầu tiêu thụ là
Qua năm thứ ba trữ lượng dầu tiêu thụ là
……
Qua năm thứ n trữ lượng dầu tiêu thụ là
Vậy tổng lượng dầu tiêu thụ trong n năm là:
Do đó ta có phương trình:
Vậy sau 41 năm, trừ lượng dầu gần như sẽ hết và không đủ dùng cho năm tới
Câu 24:
21/07/2024Hàm số có tập xác định D = R khi
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Hàm số có tập xác định D = R khi
Đặt
Khi đó (1) trở thành
Đặt
YCBT xảy ra khi
Câu 25:
22/07/2024Tìm tích tất cả các nghiệm của phương trình 4.3log(100x2)+9.4log(10x)=13.61+logx
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:

Suy ra tích các nghiệm bằng 1.
Câu 26:
20/07/2024Cho xlogα(αx)≥(αx)4
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
ĐK:
Ta có:
Đặt
(thỏa mãn điều kiện)
Câu 27:
14/07/2024Với giá trị nào của x để hàm số đạt giá trị lớn nhất?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Tập xác định của hàm số là
Ta có:
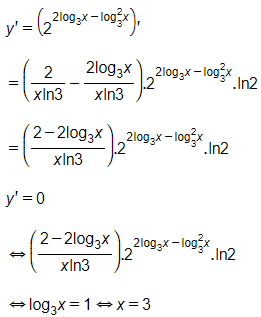
Bảng biến thiên:
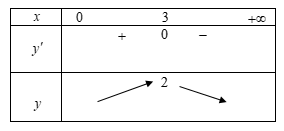
Dựa vào bảng biến thiên ta có hàm số
Câu 28:
22/07/2024Cho hàm số . Tính giá trị của biểu thức
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Ta có:
Khi đó
Do đó
Có thể bạn quan tâm
- Trắc nghiệm Ôn tập Toán 12 Chương 2 (có đáp án) (433 lượt thi)
- 200 câu trắc nghiệm Hàm số mũ và Logarit cơ bản (P1) (854 lượt thi)
- 200 câu trắc nghiệm Hàm số mũ và Logarit nâng cao (P1) (447 lượt thi)
- 40 câu trắc nghiệm: Ôn tập chương 2 có đáp án (346 lượt thi)
- Trắc nghiệm Ôn tập chương II có đáp án (Nhận biết) (315 lượt thi)
- Trắc nghiệm Ôn tập chương II có đáp án (Phần 1) (326 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Logarit có đáp án (Thông hiểu) (1219 lượt thi)
- Trắc nghiệm Logarit có đáp án (Nhận biết) (745 lượt thi)
- Trắc nghiệm Logarit (có đáp án) (686 lượt thi)
- Trắc nghiệm Lũy thừa có đáp án (Nhận biết) (595 lượt thi)
- Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit (có đáp án) (584 lượt thi)
- Trắc nghiệm Lũy thừa có đáp án (Vận dụng) (577 lượt thi)
- Trắc nghiệm Lũy thừa (có đáp án) (522 lượt thi)
- Trắc nghiệm Logarit có đáp án (518 lượt thi)
- Trắc nghiệm Logarit có đáp án (Vận dụng) (512 lượt thi)
- Trắc nghiệm Hàm số mũ. Hàm số Logarit (có đáp án) (501 lượt thi)
