20 câu hỏi trắc nghiệm thuộc Trắc nghiệm Hàm số mũ. Hàm số Logarit có đáp án (Nhận biết)

Câu 1:

17/07/2024

Hàm số $y = a^{x} (0 < a \neq 1)$ đồng biến khi nào?

A. a>1

B. 0<a<1

C. $a \geq 1$

D. a>0

Xem đáp án

Hàm số mũ $y = a^{x} (0 < a \neq 1)$ đồng biến khi a>1.

Đáp án cần chọn là: A.

Câu 2:

19/11/2024

Hàm số nào dưới đây đồng biến trên R?

A. $y = {(\frac{\sqrt{2}}{2})}^{x}$

B. $y = {(\sqrt{3} - 1)}^{x}$

C. $y = {(\frac{1}{2})}^{x}$

D. $y = 3^{2 x}$

Xem đáp án

Đáp án đúng: D

*Lời giải:

Các hàm số ở mỗi đáp án A,B,C đều có hệ số 0<a<1 nên chúng nghịch biến trên R.

Hàm số $y = 3^{2 x}$ có 3>1 nên nó đồng biến trên R.

*Phương pháp giải:

- Tìm điều kiện cho hàm số đó xác định rồi xét sự đồng biến/nghịch biến của hàm số đó

*Các dạng bài tập thường gặp sự đồng biến/nghịch biến của hàm số:

a) Dạng 1: Tìm các khoảng đơn điệu của hàm số.

* Phương pháp làm bài:

– Bước 1: Tìm tập xác định của hàm số đã cho.

– Bước 2: Tính đạo hàm f′(x) , sau đó tìm các điểm x1,x2,…,xn mà tại đó đạo hàm của hàm số bằng 0 hoặc không xác định.

– Bước 3: Xét dấu đạo hàm và đưa ra kết luận về khoảng đồng biến và nghịch biến của hàm số.

+ Các khoảng mà f′(x)>0 là các khoảng đồng biến của hàm số.

+ Các khoảng mà f′(x)<0 là các khoảng nghịch biến của hàm số.

b) Dạng 2: Tìm giá trị của m để hàm số đơn điệu trên R.

* Phương pháp làm bài:

– Bước 1: Tính f′(x).

– Bước 2: Nêu các điều kiện của bài toán:

+ Hàm số y=f(x) đồng biến trên R⇔y′=f′(x)⩾0,với ∀x∈R và y′=0 tại một hữu hạn điểm.

+ Hàm số y=f(x) nghịch biến trên R⇔y′=f′(x)⩽0,với ∀x∈R và y′=0 tại một hữu hạn điểm.

– Bước 3: Từ các điều kiện trên sử dụng các kiến thức về dấu của nhị thức bậc nhất và tam thức bậc hai để tìm m.

c) Dạng 3: Tìm m để hàm số đơn điệu trên miền D đã cho trước.

* Phương pháp làm bài:

– Bước 1: Nêu các điều kiện để hàm số đơn điệu trên D:

+ Hàm số y=f(x) đồng biến trên D⇔y′=f′(x)⩾0, với ∀x∈D.

+ Hàm số y=f(x) nghịch biến trên D⇔y′=f′(x)⩽0,với ∀x∈D.

– Bước 2: Từ điều kiện trên hãy sử dụng các cách suy luận khác nhau cho từng bài toán để tìm m.

- Bước 3: Kết luận

d) Dạng 4: Tìm m để hàm số đồng biến, nghịch biến trên khoảng

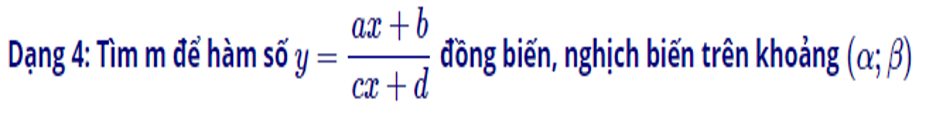
– Bước 1: Tính y′

– Bước 2: Nêu điều kiện để hàm số đồng biến và nghịch biến:

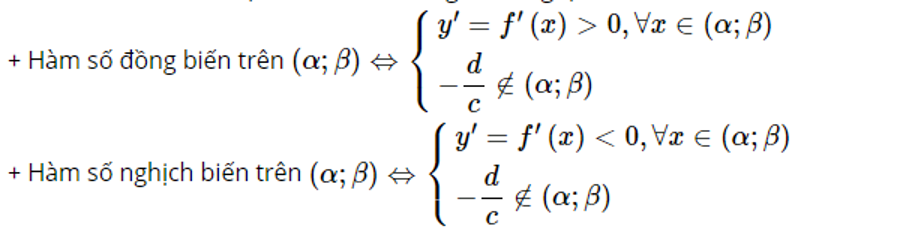
– Bước 3: Đưa ra kết luận.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Sự đồng biến, nghịch biến của hàm số (mới 2024 + Bài Tập) – Toán 12

Trắc nghiệm Sự đồng biến, nghịch biến của hàm số (có đáp án)

Bài tập Sự đồng biến nghịch biến của hàm số Toán 12 mới nhất

Câu 3:

23/07/2024

Chọn khẳng định đúng:

A. Đồ thị hàm số $y = a^{x} (0 < a \neq 1)$ đi qua điểm (0;0)

B. Đồ thị hàm số $y = a^{x} (0 < a \neq 1)$ có tiệm cận đứng x=0

C. Đồ thị hàm số $y = a^{x} (0 < a \neq 1)$ cắt trục hoành tại duy nhất 1 điểm.

D. Đồ thị hàm số $y = a^{x} (0 < a \neq 1)$ nằm hoàn toàn phía trên trục hoành

Xem đáp án

Đồ thị hàm số $y = a^{x} (0 < a \neq 1)$ nằm hoàn toàn phía trên trục hoành.

Đáp án cần chọn là: D.

Câu 4:

20/07/2024

Tập xác định của hàm số $y = 2^{x}$ là:

A. $[0; + \infty)$

B. R

C. $(0; + \infty)$

D. R*

Xem đáp án

Tập xác định của hàm số $y = 2^{x}$ là R.

Đáp án cần chọn là: B.

Câu 5:

23/07/2024

Hàm số $y = \log_{a} x (0 < a \neq 1)$ xác định trên:

A. (0;1)

B. R

C. $R \ \{0\}$

D. $(0; + \infty)$

Xem đáp án

Hàm số $y = \log_{a} x (0 < a \neq 1)$ xác định trên $(0; + \infty)$

Đáp án cần chọn là: D.

Câu 6:

16/07/2024

Cho hàm số $y = \log_{a} x$ . Nếu 0<a<1 thì hàm số:

A. Nghịch biến trên $(0; + \infty)$

B. Đồng biến trên $(0; + \infty)$

C. Nghịch biến trên $(- \infty; 0)$

D. Đồng biến trên $(- \infty; 0)$

Xem đáp án

Hàm số $y = \log_{a} x$ nghịch biến trên $(0; + \infty)$ nếu 0<a<1 và đồng biến trên $(0; + \infty)$ nếu a > 1.

Đáp án cần chọn là: A.

Câu 7:

23/07/2024

Hàm số nào sau đây đồng biến trên khoảng $(0; + \infty)$

A. $y = \log_{\frac{\sqrt{2}}{2}} x$

B. $y = \log_{\frac{e}{3}} x$

C. $y = \log_{\frac{e}{2}} x$

D. $y = \log_{\frac{x}{4}} x$

Xem đáp án

Trong các hàm số đã cho chỉ có hàm số $y = \log_{\frac{e}{2}} x$ đồng biến vì cơ số $a = \frac{e}{2} > 1$

Đáp án cần chọn là: C.

Câu 8:

12/07/2024

Điểm $(x_{0}; y_{0})$ thuộc đồ thị hàm số $y = \log_{a} x (0 < a \neq 1)$ nếu:

A. $y_{0} = \log_{a} x_{0}$

B. $y_{0} = x_{0}^{a}$

C. $y_{0} = a^{x_{0}}$

D. $x_{0} = \log_{a} y_{0}$

Xem đáp án

Điểm $(x_{0}; y_{0})$ thuộc đồ thị hàm số $y = \log_{a} x (0 < a \neq 1)$ nếu $y_{0} = \log_{a} x_{0}$

Đáp án cần chọn là: A.

Câu 9:

19/07/2024

Gọi (C) là đồ thị hàm số $y = \log x$ . Tìm khẳng định đúng?

A. Đồ thị (C) có tiệm cận đứng

B. Đồ thị (C) có tiệm cận ngang

C. Đồ thị (C) cắt trục tung

D. Đồ thị (C) không cắt trục hoành

Xem đáp án

Đồ thị hàm số y=logx nhận trục tung là tiệm cận đứng.

Đồ thị hàm số không có tiệm cận ngang và cắt trục hoành tại điểm (1; 0) nên các đáp án B, C, D đều sai.

Đáp án cần chọn là: A.

Câu 10:

12/07/2024

Cho hàm số $y = 5^{x}$ có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng với (C) qua đường thẳng y = x.

A. $y = 5^{- x}$

B. $y = \log_{5} x$

C. $y = - 5^{- x}$

D. $y = - \log_{5} x$

Xem đáp án

Đồ thị hàm số $y = 5^{x}$ đối xứng với đồ thị hàm số $y = \log_{5} x$ qua đường thẳng y = x.

Đáp án cần chọn là: B

Câu 11:

20/07/2024

Hàm số nào sau đây nghịch biến trên khoảng xác định của nó?

A. $y = \log_{\frac{1}{2}} x$

B. $y = \log_{2} x$

C. $y = \log_{\sqrt{3}} x$

D. $y = \log_{\sqrt{2}} x$

Xem đáp án

Hàm số $y = \log_{\frac{1}{2}} x$ nghịch biến trên khoảng xác định của nó, do $0 < \frac{1}{2} < 1$

Đáp án cần chọn là: A.

Câu 12:

23/07/2024

Chọn khẳng định đúng:

A. Đồ thị hàm số $y = 2^{x}$ đi qua điểm (0; 0)

B. Đồ thị hàm số $y = 2^{x}$ có tiệm cận đứng x = 0

C. Đồ thị hàm số $y = 2^{x}$ cắt trục hoành tại duy nhất 1 điểm

D. Đồ thị hàm số $y = 2^{x}$ nằm hoàn toàn phía trên trục hoành

Xem đáp án

Đáp án A sai vì đồ thị hàm số $y = 2^{x}$ di qua điểm (0; 1)

Đáp án B sai vì đồ thị hàm số có tiệm cận ngang y = 0 chứ không có tiệm cận đứng.

Đáp án C sai vì đồ thị hàm số không cắt trục hoành.

Đáp án D đúng vì $2^{x} > 0, \forall x$

Đáp án cần chọn là: D.

Câu 13:

21/07/2024

Chọn mệnh đề đúng:

A. Hàm số $y = a^{- x} (0 < a \neq 1)$ đồng biến nếu a > 1

B. Hàm số $y = a^{- x} (0 < a \neq 1)$ nghịch biến nến 0 < a < 1

C. Hàm số $y = a^{- x} (0 < a \neq 1)$ đồng biến nếu 0<a<1

D. Hàm số $y = a^{- x} (0 < a \neq 1)$ luôn nghịch biến trên R

Xem đáp án

Ta có: hàm số $y = a^{- x}$ nghịch biến khi a > 1 nên các đáp án B, D đều sai.

Nên hàm số đồng biến nếu $\frac{1}{a} > 1 \Leftrightarrow 0 < a < 1$

Đáp án cần chọn là: C.

Câu 14:

23/07/2024

Chọn mệnh đề đúng:

A. Đồ thị hàm số $y = 2^{x}$ trùng với đồ thị hàm số $y = {(\frac{1}{2})}^{- x}$

B. Đồ thị hàm số $y = 2^{x}$ trùng với đồ thị hàm số $y = 2^{- x}$

C. Đồ thị hàm số $y = 2^{x}$ đối xứng với đồ thị hàm số $y = {(\frac{1}{2})}^{- x}$ qua trục hoành

D. Đồ thị hàm số $y = 2^{x}$ đối xứng với đồ thị hàm số $y = {(\frac{1}{2})}^{- x}$ qua trục tung

Xem đáp án

Ta có: $y = {(\frac{1}{2})}^{- x} = \frac{1}{{(\frac{1}{2})}^{x}} = \frac{1}{\frac{1}{2^{x}}} = 2^{x}$ nên hai hàm số $y = 2^{x}$ và $y = {(\frac{1}{2})}^{- x}$ là một. Do đó chúng có chung đồ thị.

Đáp án cần chọn là: A.

Câu 15:

18/07/2024

Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập R?

A. $y = π^{x}$

B. $y = {(\frac{1}{3})}^{x}$

C. $y = {\sqrt{3}}^{x}$

D. $y = 3^{x}$

Xem đáp án

Trong các đáp án, chỉ có đáp án B là hàm số có hệ số $a = \frac{1}{3} < 1 \Rightarrow y = {(\frac{1}{3})}^{x}$ nghịch biến trên R

Đáp án cần chọn là: B.

Câu 16:

17/07/2024

Tính đạo hàm của hàm số $y = 6^{x}$

A. $y' = \frac{6^{x}}{\ln 6}$

B. $y' = 6^{x} \ln 6$

C. $y' = 6^{x}$

D. $y = x . 6^{- 1}$

Xem đáp án

$y = 6' \Rightarrow y' = 6^{x} \ln 6$

Đáp án cần chọn là: B.

Câu 17:

23/07/2024

Chọn mệnh đề đúng:

A. Đồ thị hàm số $y = {(\frac{1}{3})}^{x}$ đối xứng với đồ thị hàm số $y = - {(\frac{1}{3})}^{x}$ qua trục tung.

B. Đồ thị hàm số $y = {(\frac{1}{3})}^{x}$ đối xứng với đồ thị hàm số $y = - {(\frac{1}{3})}^{x}$ qua trục hoành.

C. Đồ thị hàm số $y = {(\frac{1}{3})}^{x}$ đối xứng với đồ thị hàm số $y = - {(\frac{1}{3})}^{x}$ qua đường thẳng y = x.

D. Đồ thị hàm số $y = {(\frac{1}{3})}^{x}$ đối xứng với đồ thị hàm số $y = - {(\frac{1}{3})}^{x}$ tại điểm (1;0)

Xem đáp án

Vì ${(\frac{1}{3})}^{x}$ và $- {(\frac{1}{3})}^{x}$ đối nhau nên đồ thị hai hàm số đó đối xứng nhau qua Ox

Đáp án cần chọn là: B.

Câu 18:

15/07/2024

Cho $a > 0, a \neq 1$ . Tìm mệnh đề đúng trong các mệnh đề sau:

A. Tập xác định của hàm số $y = a^{x}$ là $(0; + \infty)$

B. Tập giá trị của hàm số $y = \log_{a} x$ là tập R

C. Tập giá trị của hàm số $y = a^{x}$ là tập R

D. Tập xác định của hàm số $y = \log_{a} x$ là tập R

Xem đáp án

Cho $a > 0, a \neq 1$ . Khi đó hàm số $y = a^{x}$ có tập xác định là R, tập giá trị là $(0; + \infty)$

Hàm số $y = \log_{a} x$ có tập xác định là $(0; + \infty)$ , tập giá trị là R.

Suy ra B đúng

Đáp án cần chọn là: B.

Câu 19:

15/07/2024

Tìm tập xác định D của hàm số $y = \log_{\sqrt{2}} (\frac{- 3}{2 - 2 x})$

A. $D = (- \infty; 1)$

B. $D = [1; + \infty)$

C. $D = (- \infty; 1]$

D. $D = (1; + \infty)$

Xem đáp án

Điều kiện: $\frac{- 3}{2 - 2 x} > 0 \Leftrightarrow 2 - 2 x < 0 \Leftrightarrow x > 1$

Đáp án cần chọn là: D.

Câu 20:

12/07/2024

Cho hàm số $y = - \log_{2} x$ có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng (C) qua đường thẳng y = x.

A. $y = 2^{x}$

B. $y = 2^{\frac{1}{x}}$

C. $y = 2^{- x}$

D. $y = 2^{\frac{x}{2}}$

Xem đáp án

Trước tiên ta đưa hàm số về dạng chuẩn: $y = - \log_{2} x = \log_{2^{- 1}} x = \log_{\frac{1}{2}} x$

Suy ra hàm số cần tìm là: $y = {(\frac{1}{2})}^{x} = 2^{- x}$

Đáp án cần chọn là: C.

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3