Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (Thông hiểu)
Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (Thông hiểu)
-
391 lượt thi
-
15 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
16/10/2024Trong các hình chóp, hình chóp có ít cạnh nhất có số cạnh là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
*Phương pháp giải
Nắm vững kiến thức cơ bản về một số hình chóp thường gặp để xác định được hình chóp nào có số cạnh ít nhất.
*Lời giải
Hình tứ diện là hình chóp có số cạnh ít nhất.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết, cách xác định và bài tập các tính chất hình chóp đều
Câu 2:
22/07/2024Chọn khẳng định sai trong các khẳng định sau?
 Xem đáp án
Xem đáp án
Hai mặt phẳng có một điểm chung thì chúng có thể trùng nhau. Khi đó, chúng có vô số đường thẳng chung ⇒ B sai.
Đáp án cần chọn là: B
Câu 3:
22/07/2024Trong các khẳng định sau, khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Hai mặt phẳng phân biệt không song song với nhau thì chúng có duy nhất một giao tuyến.
A sai. Nếu (P) và (Q) trùng nhau thì 2 mặt phẳng có vô số điểm chung.
Khi đó, chưa đủ điều kiện để kết luận A, B, C thẳng hàng.
B sai. Có vô số đường thẳng đi qua A khi đó B, C chưa chắc đã thuộc giao tuyến của (P) và (Q)
C sai. Hai mặt phẳng (P) và (Q) phân biệt giao nhau tại 1 giao tuyến duy nhất, nếu 3 điểm A, B, C là 3 điểm chung của 2 mặt phẳng thì A, B, C cùng thuộc giao tuyến.
Đáp án cần chọn là: D
Câu 6:
24/11/2024Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Giao tuyến của mặt phẳng (ACD) và (GAB) là:
 Xem đáp án
Xem đáp án
Đáp án đúng: B
* Lời giải:
*Phương pháp giải:
- Nắm vững lại kiến thức về đường thẳng và mặt phẳng
*Lý thuyết cần nắm và các dạng bài tập về đường thẳng và măt phẳng:
Các tính chất thừa nhận
- Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
- Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.
- Tồn tại 4 điểm không cùng thuộc một mặt phẳng.
- Nếu có một đường thẳng có 2 điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó.
- Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu d⊂(P) hoặc .
- Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu .
- Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hìnd=(P)∩(Q)h học phẳng đều đúng.
Xác định một mặt phẳng
Một mặt phẳng hoàn toàn được xác định khi biết nó đi qua 3 điểm không thẳng hàng.
Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa 1 đường thẳng không đi qua điểm đó.
Một mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.
Tính chất của hai đường thẳng song song
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.
Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì song song với nhau.
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì 3 giao tuyến đó đồng quy hoặc đôi một song song.
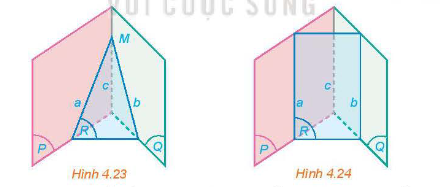
* Chú ý: Nếu hai mặt phẳng chứa 2 đường thẳng song song với nhau thì giao tuyến (nếu có) của chúng song song với 2 đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Hai mặt phẳng song song
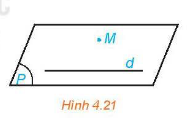
Hai mặt (α) và (β) được gọi là song song với nhau nếu chúng không có điểm chung. Kí hiệu (α)// (β) hay (β)//(α).
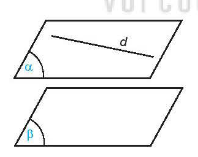
*Nhận xét: {(α)//(β)d⊂(α)⇒d//(β).
Điều kiện và tính chất của hai mặt phẳng song song
Nếu mặt phẳng (α) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng phẳng (β)thì (α)và (β)song song với nhau.
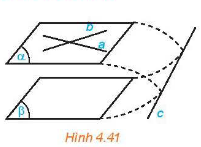
Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
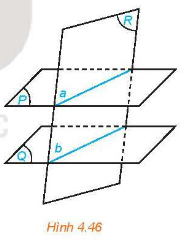
Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Đường thẳng và mặt phẳng trong không gian – Toán 11 Kết nối tri thức
Toán 11 Bài 10 (Kết nối tri thức): Đường thẳng và mặt phẳng trong không gian
Câu 10:
22/07/2024Giả sử M là giao của đường thẳng a và mặt phẳng (P). Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Nếu đường thẳng a cắt mặt phẳng (P) tại M thì .
Hơn nữa, các mặt phẳng chứa a thì cũng chứa M nên chúng đều có điểm chung với (P) do đó đều cắt (P)
Đáp án cần chọn là: B
Câu 15:
22/07/2024Gọi M là giao điểm của đường thẳng a và mặt phẳng (P). Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Nếu M là giao điểm của a và (P):
Lấy mặt phẳng (Q) bất kỳ chứa cắt (P) theo giao tuyến là đường thẳng d
Giao điểm của d và a là M
Khẳng định A là đúng
Đáp án cần chọn là: A
Có thể bạn quan tâm
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng (có đáp án) (543 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (400 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (Nhận biết) (391 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (Thông hiểu) (390 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (Vận dụng) (396 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Đường thẳng - Mặt phẳng trong không gian (P1) (1343 lượt thi)
- 100 câu trắc nghiệm Đường thẳng, Mặt phẳng trong không gian nâng cao (phần 1) (1192 lượt thi)
- Trắc nghiệm Đường thẳng và mặt phẳng song song (có đáp án) (1107 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song (có đáp án) (968 lượt thi)
- Trắc nghiệm Hai mặt phẳng song song (có đáp án) (720 lượt thi)
- Trắc nghiệm Phép chiếu song song. Hình biểu diễn của một hình không gian (có đáp án) (523 lượt thi)
- Trắc nghiệm Ôn chương 2 - hình học (có đáp án) (520 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án (506 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án (Vận dụng) (404 lượt thi)
- Trắc nghiệm Đường thẳng và mặt phẳng song song có đáp án (Nhận biết) (394 lượt thi)
