Trắc nghiệm Các dạng toán về phép nhân và phép chia phân số (có đáp án)
Trắc nghiệm Các dạng toán về phép nhân và phép chia phân số (có đáp án)
-
321 lượt thi
-
27 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 2:
23/07/2024Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án A: (−76)2=(−7)262=4936≠−4936 nên A sai.
Đáp án B: (23)3=2333=827≠89 nên B sai.
Đáp án C: (2−3)3=23(−3)3=8−27 nên C đúng.
Đáp án D: (−23)4=(−2)434=1681≠−1681 nên D sai.
Đáp án cần chọn là: C
Câu 3:
23/07/2024Tìm số nguyên x biết −56.12025<x<−715.914
 Xem đáp án
Xem đáp án
−56.12025<x<−715.914
−56.245<x<−15.32
−4<x<−310
x∈{−3;−2;−1}
Đáp án cần chọn là: A
Câu 4:
23/07/2024Có bao nhiêu giá trị nguyên dương của x thỏa mãn (−53)3<x<−2435.−56 ?
 Xem đáp án
Xem đáp án
Vì x nguyên dương nên x >0
mà (−53)3=−12527<0 nên (−53)3<0<x<−2435.−56
Khi đó: 0<x<−2435.−56
0<x<47
Vì 47<1 nên 0 < x < 1 nên không có số nguyên dương nào thỏa mãn.
Đáp án cần chọn là: B
Câu 5:
23/07/2024Có bao nhiêu giá trị của x thỏa mãn (76+x):1625=−54 ?
 Xem đáp án
Xem đáp án
(76+x):1625=−54
76+x=−54.1625
76+x=−11.45
76+x=−45
x=−45−76x=−5930
Đáp án cần chọn là: C
Câu 6:
23/07/2024Cho M=175.−31125.12.1017.(−12)3 và N=(1728+2829−1930−2031).(−512+14+16) . Khi đó tổng M + N bằng
 Xem đáp án
Xem đáp án
M=175.−31125.12.1017.(−12)3
M=17.(−31).1.10.(−1)35.125.2.17.23
M=−31.(−1)125.23
M=311000
N=(1728+2829−1930−2031).(−512+14+16)
N=(1728+2829−1930−2031).(−512+312+212)
N=(1728+2829−1930−2031).0
N = 0
Vậy M+N=311000+0=311000
Đáp án cần chọn là: B
Câu 7:
23/07/2024Tính B=223⋅328⋅4215⋅5224⋅6235⋅7248⋅8263⋅9280 ta được
 Xem đáp án
Xem đáp án
B=223⋅328⋅4215⋅5224⋅6235⋅7248⋅8263⋅9280
=2.21.3⋅3.32.4⋅4.43.5⋅5.54.6⋅6.65.7⋅7.76.8⋅8.87.9⋅9.98.10
=2.3.4.5.6.7.8.91.2.3.4.5.6.7.8.⋅2.3.4.5.6.7.8.93.4.5.6.7.8.9.10
=91⋅210=9.21.10=95
Đáp án cần chọn là: A
Câu 8:
23/07/2024Tính giá trị biểu thức A=(114.−59−49.114).833
 Xem đáp án
Xem đáp án
Ta có: A=(114.−59−49.114).833=114.(−59−49).833=114.−99.833=−114.833=−23
Đáp án cần chọn là: A
Câu 9:
23/07/2024Tìm số tự nhiên x biết 13+16+110+...+1x(x+1):2=20192021
 Xem đáp án
Xem đáp án
13+16+110+...+1x(x+1):2=20192021
2[12.3+13.4+...+1x(x+1)]=20192021
2.(12−13+13−14+...+1x−1x+1)=20192021
2(12−1x+1)=20192021
1−2x+2=20192021
2x+1=1−20192021
2x+1=22021x+1=2021x=2020
Đáp án cần chọn là: C
Câu 10:
23/07/2024Tìm M=1+12+122+123+...+1299+12100
 Xem đáp án
Xem đáp án
M=1+12+122+123+...+1299+121002M=2.(1+12+122+123+...+1299+12100)=2+1+12+122+123+...+1299
Ta có:
M=2M−M
=(2+1+12+122+123+...+1298+1299)−(1+12+122+123+...+1299+12100)
=2−12100
=2101−12100
Đáp án cần chọn là: D
Câu 11:
23/07/2024Tính diện tích một hình tam giác biết hai cạnh góc vuông của tam giác đó lần lượt là 53 cm và 74 cm?
 Xem đáp án
Xem đáp án
Diện tích hình tam giác đó là: S=12.53.74=1.5.72.3.4=3524cm2
Đáp án cần chọn là: C
Câu 12:
23/07/2024Một hình chữ nhật có diện tích 4835 m2và có chiều dài là 65 m. Tính chiều rộng của hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Chiều rộng của hình chữ nhật là:
4835:65=4835.56=6.87.5.56=87 (m)
Đáp án cần chọn là: A
Câu 13:
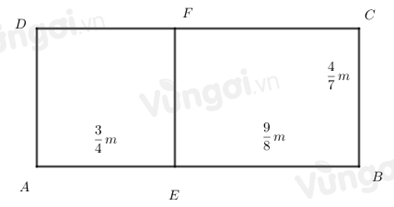
23/07/2024Tính diện tích hình chữ nhật ABCD ở hình sau:
 Xem đáp án
Xem đáp án
Cách 1:
Chiều dài hình chữ nhật ABCD là:
34+98=158(m)
Diện tích hình chữ nhật ABCD là:
47.158=1514(m2)
Cách 2:
Diện tích hình chữ nhật ADFE là:
34.47=37(m2)
Diện tích hình chữ nhật BCFE là:
47.98=914(m2)
Diện tích hình chữ nhật ABCD là:
37+914=1514(m2)
Đáp án cần chọn là: A
Câu 14:
23/07/2024
Điền số thích hợp vào ô trống
Chim ruồi ong hiện là loài chim bé nhỏ nhất trên Trái Đất với chiều dài chỉ khoảng 5 cm. Chim ruồi “khổng lồ” ở Nam Mỹ là thành viên lớn nhất của gia đình chim ruồi trên thế giới, nó dài gấp 338 lần chim ruồi ong. Chiều dài của chim ruồi “khổng lồ” ở Nam Mỹ là  cm
cm
 Xem đáp án
Xem đáp án
Chim ruồi ong hiện có chiều dài khoảng 5 cm.
Chim ruồi "khổng lồ" ở Nam Mỹ dài gấp 338 lần chim ruồi ong.
Chiều dài của chim ruồi "khổng lồ" ở Nam Mỹ là:
338.5=33.58=1658=20,625(cm)
Câu 15:
13/12/2024Tính 2815.142.3+(815−6960.523):5154
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Lời giải
2815.142.3+(815−6960.523):5154
=28.1.315.42+(815−23.34.3.5.523).5451
=7.4.1.33.5.4.4+(815−14).5451=720+(3260−1560).5451=720+1760.5451=720+176.10.6.3.317.3=720+310=720+620=1320
*Phương pháp giải:
Áp dụng phép toán với số thập phân
*Lý thuyết:
1. Ôn lại phân số thập phân
Các phân số có mẫu số là 10; 100; 1000;... được gọi là các phân số thập phân.
Ví dụ: 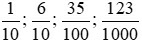 là các phân số thập phân.
là các phân số thập phân.
2. Khái niệm số thập phân, cấu tạo số thập phân
2.1. Khái niệm số thập phân
|
m |
dm |
cm |
mm |
|
0 |
1 |
|
|
|
0 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
+) 1dm hay 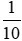 m còn viết thành 0,1m
m còn viết thành 0,1m
+) 1cm hay 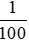 m còn viết thành 0,01m
m còn viết thành 0,01m
+) 1mm hay 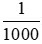 m còn viết thành 0,001m
m còn viết thành 0,001m
Các phân số thập phân 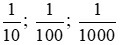 được viết thành 0,1; 0,01; 0,001.
được viết thành 0,1; 0,01; 0,001.
0,1 đọc là: không phẩy một: 0,1 =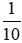
0,01 đọc là: không phẩy không một: 0,01 =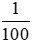
0,001 đọc là: không phẩy không không một: 0,001 =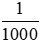
Các số 0,1; 0,01; 0,001 được gọi là số thập phân.
Tương tự, các phân số thập phân 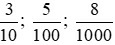 được viết thành 0,3; 0,05; 0,008.
được viết thành 0,3; 0,05; 0,008.
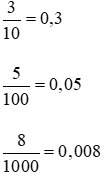
Các số 0,3; 0,05; 0,008 cũng là số thập phân.
2.2. Cấu tạo số thập phân
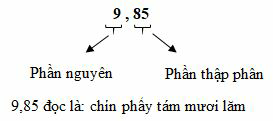
Mỗi số thập phân gồm hai phần: phần nguyên và phần thập phân, chúng được phân cách bởi dấu phẩy.
Những chữ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên phải dấu phẩy thuộc về phần thập phân.
Ví dụ:
Xem thêm
Câu 16:
23/07/2024Phân số nghịch đảo của số −3 là
 Xem đáp án
Xem đáp án
Phân số nghịch đảo của số −3 là 1−3
Đáp án cần chọn là: C
Câu 17:
23/07/2024Kết quả của phép tính (−7)6:(−143) là phân số có tử số là
 Xem đáp án
Xem đáp án
(−7)6:(−143)=−76.−314=1.12.2=14
Đáp án cần chọn là: D
Câu 18:
23/07/2024Giá trị nào dưới đây của x thỏa mãn (−35).x=415
 Xem đáp án
Xem đáp án
(−35).x=415x=415:(−35)x=415.5−3x=−49
Đáp án cần chọn là: B
Câu 19:
23/07/2024Giá trị biểu thức M=56:(52)2+715 là phân số tối giản có dạng ab với a >0. Tính b + a.
 Xem đáp án
Xem đáp án
M=56:(52)2+715
M=56:254+715
M=56.425+715
M=1.23.5+715
M=215+715
M=915=35
Khi đó a = 3, b = 5 nên a + b = 8
Đáp án cần chọn là: A
Câu 20:
23/07/2024Rút gọn N=417−449−4131317−349−3131 ta được
 Xem đáp án
Xem đáp án
N=417−449−4131317−349−3131=4.117−4.149−4.11313.117−3.149−3.1131=4.(117−149−1131)3.(117−149−1131)=43
Đáp án cần chọn là: A
Câu 21:
23/07/2024Tìm x biết (x+14−13):(2+16−14)=746
 Xem đáp án
Xem đáp án
(x+14−13):(2+16−14)=746
(x+14−13):2312=746
x+14−13=746.2312
x+14−13=724
x=724−14+13
x=38
Đáp án cần chọn là: D
Câu 22:
23/07/2024Giá trị của x thỏa mãn 1315−(1321+x).712=710 ?
 Xem đáp án
Xem đáp án
1315−(1321+x).712=710
(1321+x).712=1315−710
(1321+x).712=16
1321+x=16:712
1321+x=27
x=27−1321
x=−13
Đáp án cần chọn là: A
Câu 23:
23/07/2024Số các số nguyên x để 5x3:10x2+5x21 có giá trị là số nguyên là
 Xem đáp án
Xem đáp án
5x3:10x2+5x21=5x3.2110x2+5x=5x.213.5x.(2x+1)=72x+1
Để biểu thức đã cho có giá trị là số nguyên thì 72x+1 nguyên
Do đó 2x + 1 ∈ Ư(7) = {±1; ±7}
Ta có bảng:

Vậy x ∈ {0; −1; 3; −4} suy ra có 4 giá trị thỏa mãn.
Đáp án cần chọn là: B
Câu 24:
22/07/2024Một người đi xe máy, đi đoạn đường AB với vận tốc 40km/h hết 54 giờ. Lúc về, người đó đi với vận tốc 45km/h. Tính thời gian người đó đi từ B về A?
 Xem đáp án
Xem đáp án
Quãng đường AB là: 40.54=50 (km)
Thời gian người đó đi từ B về A là: 5045=109 (giờ)
Đáp án cần chọn là: A
Câu 25:
23/07/2024Phân số ab là phân số lớn nhất mà khi chia mỗi phân số 1235;1849 cho ab ta được kết quả là một số nguyên. Tính a + b.
 Xem đáp án
Xem đáp án
Gọi phân số lớn nhất cần tìm là: ab (a;b là nguyên tố cùng nhau)
Ta có: 1235:ab=12b35a là số nguyên, mà 12; 35 là nguyên tố cùng nhau
Nên 12 ⋮ a; b ⋮ 3
Ta lại có: 1849:ab=18b49a là số nguyên, mà 18 và 49 nguyên tố cùng nhau
Nên 18 ⋮ a; b ⋮ 49
Để ab lớn nhất ta có a = UCLN(12; 18) = 6a và b = BCNN(35; 49)= 245b
Vậy tổng a + b = 6 + 245 = 251
Đáp án cần chọn là: B
Câu 26:
23/07/2024
Điền số thích hợp vào ô trống:
Một ô tô chạy hết 34 giờ trên một đoạn đường với vận tốc trung bình 40km/h.
Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ 12 giờ thì ô tô phải chạy với vận tốc trung bình là:  km/h
km/h
 Xem đáp án
Xem đáp án
Quãng đường ô tô đi được là: S=vtb.t=40.34=30(km)
Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ 12 giờ thì ô tô phải chạy với vận tốc trung bình là:vtb=s:t=30:12=60(km/h)
Câu 27:
23/07/2024Tính giá trị biểu thức:
(−2−5:3−4).45
 Xem đáp án
Xem đáp án
(−2−5:3−4).45=(25.−43).45=−815.45=−3275
Đáp án cần chọn là: C
Có thể bạn quan tâm
- Trắc nghiệm Phép nhân và phép chia phân số (có đáp án) (284 lượt thi)
- Trắc nghiệm Các dạng toán về phép nhân và phép chia phân số (có đáp án) (320 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm So sánh phân số (có đáp án) (419 lượt thi)
- Trắc nghiệm Giá trị phân số của một số (có đáp án) (340 lượt thi)
- Trắc nghiệm Tính chất cơ bản của phân số (có đáp án) (317 lượt thi)
- Trắc nghiệm Hỗn số (có đáp án) (292 lượt thi)
- Trắc nghiệm Phép cộng và phép trừ phân số (có đáp án) (274 lượt thi)
- Trắc nghiệm Bài tập ôn tập chương 5: Phân số (có đáp án) (264 lượt thi)
- Trắc nghiệm Phân số với tử số và mẫu số là số nguyên (có đáp án) (256 lượt thi)
- Trắc nghiệm Các dạng toán về phân số với tử số và mẫu số là số nguyên (có đáp án) (246 lượt thi)
- Trắc nghiệm Các dạng toán về phép cộng và phép trừ phân số (có đáp án) (245 lượt thi)
