Câu hỏi:
13/12/2024 5,796Tính \[\frac{{28}}{{15}}.\frac{1}{{{4^2}}}.3 + \left( {\frac{8}{{15}} - \frac{{69}}{{60}}.\frac{5}{{23}}} \right):\frac{{51}}{{54}}\]
A. \[\frac{1}{3}\]
B. \[\frac{{20}}{{13}}\]
C. 3
D. \[\frac{{13}}{{20}}\]
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là D
Lời giải
\[\frac{{28}}{{15}}.\frac{1}{{{4^2}}}.3 + \left( {\frac{8}{{15}} - \frac{{69}}{{60}}.\frac{5}{{23}}} \right):\frac{{51}}{{54}}\]
\( = \frac{{28.1.3}}{{{{15.4}^2}}} + \left( {\frac{8}{{15}} - \frac{{23.3}}{{4.3.5}}.\frac{5}{{23}}} \right).\frac{{54}}{{51}}\)
\(\begin{array}{l} = \frac{{7.4.1.3}}{{3.5.4.4}} + \left( {\frac{8}{{15}} - \frac{1}{4}} \right).\frac{{54}}{{51}}\\ = \frac{7}{{20}} + \left( {\frac{{32}}{{60}} - \frac{{15}}{{60}}} \right).\frac{{54}}{{51}}\\ = \frac{7}{{20}} + \frac{{17}}{{60}}.\frac{{54}}{{51}}\\ = \frac{7}{{20}} + \frac{{17}}{{6.10}}.\frac{{6.3.3}}{{17.3}}\\ = \frac{7}{{20}} + \frac{3}{{10}}\\ = \frac{7}{{20}} + \frac{6}{{20}}\\ = \frac{{13}}{{20}}\end{array}\)
*Phương pháp giải:
Áp dụng phép toán với số thập phân
*Lý thuyết:
1. Ôn lại phân số thập phân
Các phân số có mẫu số là 10; 100; 1000;... được gọi là các phân số thập phân.
Ví dụ: 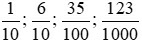 là các phân số thập phân.
là các phân số thập phân.
2. Khái niệm số thập phân, cấu tạo số thập phân
2.1. Khái niệm số thập phân
|
m |
dm |
cm |
mm |
|
0 |
1 |
|
|
|
0 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
+) 1dm hay 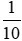 m còn viết thành 0,1m
m còn viết thành 0,1m
+) 1cm hay 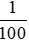 m còn viết thành 0,01m
m còn viết thành 0,01m
+) 1mm hay 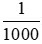 m còn viết thành 0,001m
m còn viết thành 0,001m
Các phân số thập phân 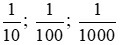 được viết thành 0,1; 0,01; 0,001.
được viết thành 0,1; 0,01; 0,001.
0,1 đọc là: không phẩy một: 0,1 =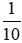
0,01 đọc là: không phẩy không một: 0,01 =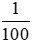
0,001 đọc là: không phẩy không không một: 0,001 =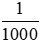
Các số 0,1; 0,01; 0,001 được gọi là số thập phân.
Tương tự, các phân số thập phân 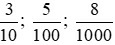 được viết thành 0,3; 0,05; 0,008.
được viết thành 0,3; 0,05; 0,008.
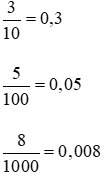
Các số 0,3; 0,05; 0,008 cũng là số thập phân.
2.2. Cấu tạo số thập phân
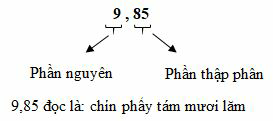
Mỗi số thập phân gồm hai phần: phần nguyên và phần thập phân, chúng được phân cách bởi dấu phẩy.
Những chữ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên phải dấu phẩy thuộc về phần thập phân.
Ví dụ:
Xem thêm
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Rút gọn \[N = \frac{{\frac{4}{{17}} - \frac{4}{{49}} - \frac{4}{{131}}}}{{\frac{3}{{17}} - \frac{3}{{49}} - \frac{3}{{131}}}}\] ta được
Câu 3:
Có bao nhiêu giá trị của x thỏa mãn \[\left( {\frac{7}{6} + x} \right):\frac{{16}}{{25}} = \frac{{ - 5}}{4}\] ?
Câu 4:
Phân số \(\frac{a}{b}\) là phân số lớn nhất mà khi chia mỗi phân số \(\frac{{12}}{{35}};\frac{{18}}{{49}}\) cho \(\frac{a}{b}\) ta được kết quả là một số nguyên. Tính a + b.
Câu 5:
Tính diện tích một hình tam giác biết hai cạnh góc vuông của tam giác đó lần lượt là \(\frac{5}{3}\) cm và \(\frac{7}{4}\) cm?
Câu 6:
Giá trị nào dưới đây của x thỏa mãn \[\left( { - \frac{3}{5}} \right).x = \frac{4}{{15}}\]
Câu 7:
Tìm x biết \[\left( {x + \frac{1}{4} - \frac{1}{3}} \right):\left( {2 + \frac{1}{6} - \frac{1}{4}} \right) = \frac{7}{{46}}\]
Câu 9:
Tính \[B = \frac{{{2^2}}}{3} \cdot \frac{{{3^2}}}{8} \cdot \frac{{{4^2}}}{{15}} \cdot \frac{{{5^2}}}{{24}} \cdot \frac{{{6^2}}}{{35}} \cdot \frac{{{7^2}}}{{48}} \cdot \frac{{{8^2}}}{{63}} \cdot \frac{{{9^2}}}{{80}}\] ta được
Câu 10:

Điền số thích hợp vào ô trống
Chim ruồi ong hiện là loài chim bé nhỏ nhất trên Trái Đất với chiều dài chỉ khoảng 5 cm. Chim ruồi “khổng lồ” ở Nam Mỹ là thành viên lớn nhất của gia đình chim ruồi trên thế giới, nó dài gấp \(\frac{{33}}{8}\) lần chim ruồi ong. Chiều dài của chim ruồi “khổng lồ” ở Nam Mỹ là  cm
cm
Câu 12:

Điền số thích hợp vào ô trống:
Một ô tô chạy hết \(\frac{3}{4}\) giờ trên một đoạn đường với vận tốc trung bình 40km/h.
Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ \(\frac{1}{2}\) giờ thì ô tô phải chạy với vận tốc trung bình là:  km/h
km/h
Câu 13:
Có bao nhiêu giá trị nguyên dương của x thỏa mãn \[{\left( {\frac{{ - 5}}{3}} \right)^3} < x < \frac{{ - 24}}{{35}}.\frac{{ - 5}}{6}\] ?
Câu 14:
Tính giá trị biểu thức \[A = \left( {\frac{{11}}{4}.\frac{{ - 5}}{9} - \frac{4}{9}.\frac{{11}}{4}} \right).\frac{8}{{33}}\]
Câu 15:
Cho \[M = \frac{{17}}{5}.\frac{{ - 31}}{{125}}.\frac{1}{2}.\frac{{10}}{{17}}.{\left( {\frac{{ - 1}}{2}} \right)^3}\] và \[N = \left( {\frac{{17}}{{28}} + \frac{{28}}{{29}} - \frac{{19}}{{30}} - \frac{{20}}{{31}}} \right).\left( {\frac{{ - 5}}{{12}} + \frac{1}{4} + \frac{1}{6}} \right)\] . Khi đó tổng M + N bằng