50 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi thptqg môn Toán cực hay mới nhất (Đề số 07)

Một ô tô đang chạy đều với vận tốc 15m/s thì phía trước xuất hiện chướng ngại vật nên người lái đạp phanh gấp. Kể từ thời điểm đó, ô tô chuyển động chậm dần đều với gia tốc $a (m / s^{2}) .$ Biết ôtô chuyển động được thêm 30m thì dừng hẳn. Hỏi a thuộc khoảng nào dưới đây?

A. (4;5)

B. (2;3)

C. (5;6)

D. (3;5)

Xem đáp án

Câu 4:

Cho hàm số $y = (x^{2} + 2 x - 2) e^{x} .$ Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên [0;1] bằng bao nhiêu?

A. -2e

B. 2e

C. e

D. -e

Xem đáp án

Câu 5:

09/07/2024

Trong không gian với hệ trục tọa độ Oxyz, gọi $(α)$ là mặt phẳng cắt ba trục tọa độ tại ba điểm $A (2; 0; 0), B (0; 3; 0), C (0; 0; 1) .$ Phương trình của $(α)$ là

A. $\frac{x}{2} + \frac{y}{3} + \frac{z}{1} = 1$

B. $3 x + 2 y - 6 z = 0$

C. $\frac{x}{2} = \frac{y}{3} = \frac{z}{1}$

D. $\frac{x}{2} + \frac{y}{3} + \frac{z}{1} = 0$

Xem đáp án

Đáp án A

Phương trình theo đoạn chắn của mặt phẳng $(α)$ là $\frac{x}{2} + \frac{y}{3} + \frac{z}{1} = 1$

Câu 6:

09/07/2024

Mặt phẳng $(P) : x - 2 z + 1 = 0$ có một véctơ pháp tuyến là

A. $\vec{n} = (1; - 2; 0)$

B. $\vec{n} = (1; 0; - 2)$

C. $\vec{n} = (- 2; 1; 0)$

D. $\vec{n} = (2; 0; 3)$

Xem đáp án

Đáp án B

Mặt phẳng $(P) : x - 2 z + 1 = 0$ nhận $\vec{n} = (1; 0; - 2)$ là một véctơ pháp tuyến

Câu 7:

Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = |x|$ , trục tung, trục hoành và đường thẳng x = 1 là

A. $\frac{3}{2}$

B. 1

C. 2

D. $\frac{1}{2}$

Xem đáp án

Câu 8:

07/07/2024

Tìm m để hàm số $y = f (x) = \{\begin{cases} \frac{\sqrt{x^{2} + 3 x} - 2}{x - 1} khix > 1 \\ mx + 2 khix \leq 1 \end{cases}$ liên tục tại $x = 1$ .

A. m = -3

B. m = $- \frac{3}{4}$

C. m = $\frac{3}{4}$

D. m = $- \frac{3}{2}$

Xem đáp án

Câu 9:

Đường thẳng y = x + m cắt đồ thị hàm số $y = \frac{x}{x - 1}$ tại hai điểm phân biệt khi

A. $0 < m < 4$

B. $m \in ℝ$

C. $- 4 < m < 0$

D. $x \neq 1$

Xem đáp án

Câu 10:

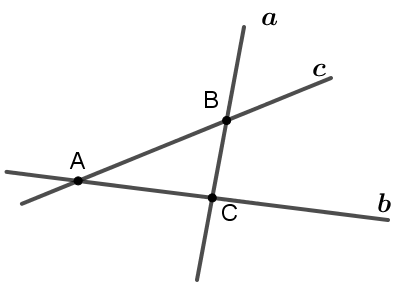
Cho ba đường thẳng a, b, c đôi một cắt nhau và không đồng phẳng. Tìm số giao điểm phân biệt của ba đường thẳng đã cho.

A. 6

B. 2

C. 1

D. 3

Xem đáp án

Đáp án C

Nếu ba đường thẳng a,b,c đôi một cắt nhau và không đồng phẳng thì chúng chỉ có thể đồng quy tại một điểm.

Câu 11:

Tìm tập giá trị T của hàm số $1 + 2 |\sin 2 x|$ .

A. $T = [1; 3]$

B. $T = [- 1; 3]$

C. $T = ℝ$

D. $T = [- 3; 3]$

Xem đáp án

Câu 12:

14/07/2024

Trên mặt phẳng tọa độ các điểm A,B,C lần lượt là điểm biểu diễn các số phức $i^{3}, \frac{3 - i}{1 - i}, \frac{(5 + 3 i) (1 - i)}{2} .$ Khi đó tam giác ABC.

A. vuông cân tại B

B. đều

C. vuông cân tại A

D. vuông cân tại C

Xem đáp án

Câu 13:

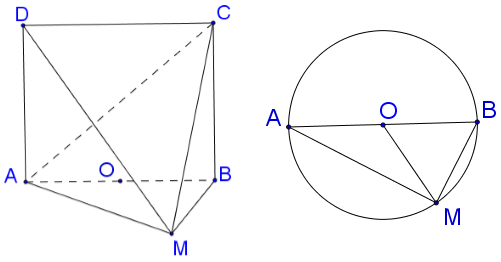
Cho hình trụ thiết diện qua trục hoành là hình vuông ABCD cạnh $4 \sqrt{3} cm$ với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung AB sao cho $\hat{ABM =} 60^{o}$ . Tính thể tích của khối tứ diện ACDM

A. $6 {cm}^{3}$

B. $24 {cm}^{3}$

C. $3 {cm}^{3}$

D. $8 {cm}^{3}$

Xem đáp án

Đáp án B

Câu 14:

12/07/2024

Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn $|z - 2 i| = 1$ là đường tròn có phương trình nào sau đây?

A. ${(x - 2)}^{2} + y^{2} = 0$

B. $x^{2} + {(y - 2)}^{2} = 0$

C. $x^{2} + {(y - 2)}^{2} = 1$

D. ${(x - 2)}^{2} + y^{2} = 1$

Xem đáp án

Câu 15:

Phương trình ${(2 - \sqrt{3})}^{x} + {(2 + \sqrt{3})}^{x} - 4 = 0$ có tổng bình phương các nghiệm là

A. 2

B. 3

C. 1

D. 0

Xem đáp án

Câu 16:

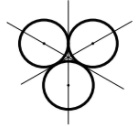
20/07/2024

Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình H. Hỏi H có mấy trục đối xứng?

A. 2

B. 1

C. 0

D. 3

Xem đáp án

Đáp án D

Có ba trục đối xứng như hình vẽ.

Câu 17:

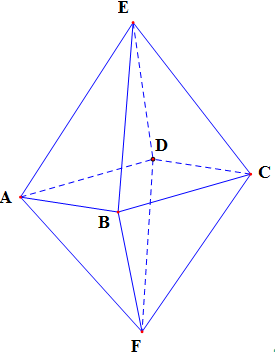
20/07/2024

Số cạnh của một hình bát diện đều là

A. 4

B. 12

C. 16

D. 8

Xem đáp án

Đáp án B

Một hình bát diện đều có 12 cạnh.

Câu 18:

Tổng các nghiệm của phương trình $2 \log_{8} 2 x + \log_{8} {(x - 1)}^{2} = \frac{4}{3}$ bằng

A. 2

B. 3

C. 5

D. 4

Xem đáp án

Đáp án A

Câu 19:

18/07/2024

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có $AB = a, BC = 3 a .$ Hai mặt phẳng (SAB) và mặt phẳng (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC hợp với mặt đáy một góc $30^{o} .$ Tính thể khối chóp S.ABCD theo a.

A. $\frac{\sqrt{30} a^{3}}{3} (dvtt)$

B. $\sqrt{10} a^{3} (dvtt)$

C. $\frac{\sqrt{10} a^{3}}{3} (dvtt)$

D. $\sqrt{30} a^{3} (dvtt)$

Xem đáp án

Câu 20:

18/07/2024

Hàm số $y = 2 \cos^{2} 2 x$ tuần hoàn với chu kì

A. $\frac{π}{2}$

B. $π$

C. $\frac{3 π}{2}$

D. $2 π$

Xem đáp án

Câu 21:

Giải bất phương trình $9^{x} - 3^{x + 1} + 3 > 1 .$

A. $0 < x < \log_{3} 2$

B. $[\begin{array}{l} x < 0 \\ x > \log_{3} 2 \end{array}$

C. $x > \log_{3} 2$

D. $x < 0$

Xem đáp án

Câu 22:

18/07/2024

Tích phân $I = \int_{1}^{2} xlnxdx$ có giá trị bằng

A. $2 \ln 2 - 2$

B. $\ln 2 - 4$

C. $2 \ln 2 - \frac{3}{4}$

D. $2 \ln 2 - \frac{5}{2}$

Xem đáp án

Câu 23:

Tính $16^{- 0, 75} + {(\frac{1}{8})}^{\frac{1}{3}} - {(\frac{1}{32})}^{\frac{3}{5}} .$

A. 4

B. 2

C. $\frac{1}{4}$

D. $\frac{1}{2}$

Xem đáp án

Câu 24:

Cho hàm số $y = \frac{3 x + 1}{3 x - 1}$ có đồ thị (C). Khẳng định nào sau đây là khẳng định

A. Đồ thị (C) có tiệm cận đứng $y = \frac{1}{3}$ và tiệm cận ngang x = 1

B. Đồ thị (C) có tiệm cận đứng $x = \frac{1}{3}$ và tiệm cận ngang y = 1

C. Đồ thị (C) có tiệm cận đứng x = -1 và tiệm cận ngang $y = \frac{1}{3}$

D. Đồ thị (C) có tiệm cận đứng $x = - \frac{1}{3}$ và tiệm cận ngang y = -1

Xem đáp án

Câu 25:

Trong không gian với hệ trục tọa độ Oxyz, cho véctơ $\vec{MN} = (- 1; 0; 2)$ và $M (1; 0; 1)$ thì tọa độ điểm N là

A. $N (0; 0; 1)$

B. $N (2; 0; - 1)$

C. $N (- 2; 0; 1)$

D. $N (0; 0; 3)$

Xem đáp án

Câu 26:

Tìm giới hạn $\lim_{x \to - \infty} \frac{\sqrt{x^{2} - x}}{x + 3}$

A. 0

B. $- \infty$

C. -1

D. 1

Xem đáp án

Câu 27:

Cho hình chóp S.ABC với $SA ⊥ SB, SB ⊥ SC, SC ⊥ SA;$ $SA = SB = SC = a .$ Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB, AC. Thể tích của hình chóp S.AB′C′ là

A. $\frac{a^{3}}{24}$

B. $a^{3}$

C. $\frac{a^{3}}{3}$

D. $\frac{a^{3}}{12}$

Xem đáp án

Câu 28:

Một hộp có 3 viên bi đỏ và 6 viên bi xanh. Lấy ngẫu nhiên 2 viên từ hộp trên. Tính xác suất để được cả 2 viên đều là bi xanh?

A. $\frac{1}{5}$

B. $\frac{2}{3}$

C. $\frac{1}{12}$

D. $\frac{5}{12}$

Xem đáp án

Câu 29:

Tính số gia Δy của hàm số $y = x^{3} - 3 x^{2}$ theo số gia của đối số Δx tại $x_{0} = 1$

A. $Δ y = {(Δ x)}^{2} - 3 Δ x$

B. $Δ y = {(Δ x)}^{3} - 3 Δ x$

C. $Δ y = {(Δ x)}^{3} - 6 Δ x$

D. $Δ y = {(Δ x)}^{3} + 3 Δ x$

Xem đáp án

Câu 30:

20/07/2024

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng $d : \{\begin{cases} x = 1 - t \\ y = 2 t \\ z = 2 + 2 t \end{cases}, t \in ℝ$ và mặt phẳng $(P) : x + y - z - 1 = 0 .$ Giao điểm M của d và (P) có tọa độ là

A. $M (1; 1; 1)$

B. $M (0; 2; 4)$

C. $M (1; 0; 2)$

D. $M (3; - 4; - 2)$

Xem đáp án

Câu 31:

14/07/2024

Tìm công thức số hạng tổng quát $(u_{n})$ biết $u_{1} = 1;, u_{n} = \frac{u_{n}}{u_{n} + 2}, \forall n \in N^{*}$

A. $u_{n} = \frac{1}{2^{n} + 1}$

B. $u_{n} = 2^{n} - 1$

C. $u_{n} = 2^{n} + 1$

D. $u_{n} = \frac{1}{2^{n} - 1}$

Xem đáp án

Câu 32:

Cho khối chóp S.ABC có $SA = a, SB = 2 a, SC = 3 a .$ Thể tích lớn nhất của khối chóp là

A. $3 a^{3} (dvtt)$

B. $\sqrt{3} a^{3} (dvtt)$

C. $2 a^{3} (dvtt)$

D. $a^{3} (dvtt)$

Xem đáp án

Câu 33:

Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm. Tính xác suất để trong 5 sản phẩm được chọn không có phế phẩm nào.

A. $\frac{1}{5}$

B. $\frac{1}{2}$

C. $\frac{2}{9}$

D. $\frac{5}{8}$

Xem đáp án

Câu 34:

Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân cạnh huyền bằng 2a. Tính thể tích của khối nón.

A. $\frac{\sqrt{2} {πa}^{3}}{3} (dvtt)$

B. $\frac{\sqrt{2} {πa}^{3}}{12} (dvtt)$

C. $\frac{\sqrt{2} {πa}^{3}}{4} (dvtt)$

D. $\frac{\sqrt{2} {πa}^{3}}{6} (dvtt)$

Xem đáp án

Câu 35:

10/07/2024

Số đường tiệm cận của đồ thị hàm số $y = \frac{3 x - 1}{\sqrt{x^{2} + x + 2}}$ là

A. 1

B. 0

C. 2

D. 3

Xem đáp án

Câu 36:

Cho tứ diện đều ABCD. Gọi G là trọng tâm tam giác ABC. Chọn khẳng định đúng trong các khẳng định sau:

A. $BG ⊥ (ACD)$

B. $DG ⊥ (ACB)$

C. $DA ⊥ (ABC)$

D. $AG ⊥ (BCD)$

Xem đáp án

Câu 37:

06/07/2024

Hàm $y = - x^{3} - 3 x^{2} + 2$ có giá trị cực tiểu $y_{C T}$ là

A. $y_{CT} = - 6$

B. $y_{CT} = - 4$

C. $y_{CT} = - 2$

D. $y_{CT} = 2$

Xem đáp án

Câu 38:

Để số phức $z = a + (1 + a) i, a \in ℝ$ có $|z| = 1$ thì

A. a = -1 hoặc a = 0

B. $a = - \frac{1}{2}$

C. $|a| = 1$

D. $a = \frac{1}{2}$

Xem đáp án

Câu 39:

13/07/2024

Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình $2 x + y - 1 = 0$ . Để phép tịnh tiến theo vecto $\vec{v}$ biến d thành chính nó thì $\vec{v}$ là vecto nào trong các vecto sau?

A. $\vec{v} = (2; 1)$

B. $\vec{v} = (1; 2)$

C. $\vec{v} = (- 2; 1)$

D. $\vec{v} = (- 1; 2)$

Xem đáp án

Đáp án D

(d) biến thành chính nó khi vecto tịnh tiến cùng phương với (d). Mà (d) có một VTCP là $(1; 2)$

Câu 40:

13/07/2024

Tìm tất cả các giá trị thực của tham số m để hàm số $y = \frac{cosx + m}{cosx - m}$ nghịch biến trên $(\frac{π}{2}, π) .$

A. $- 1 < m < 0$

B. $m \geq 0$

C. $m \leq - 1$

D. $- 1 \leq m \leq 0$

Xem đáp án

Câu 41:

08/07/2024

Số điểm biểu diễn nghiệm của phương trình $\cos^{2} x + sinxcosx + cosx - sinx = 0$ trên đường tròn lượng giác là

A. 4

B. 2

C. 1

D. 3

Xem đáp án

Đáp án C

Nhận thấy cos x = 0 không phải là nghiệm của phương trình. Chia cả hai vế của phương trình cho cosx ta được

Vậy có 1 điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác.

Câu 42:

23/07/2024

Một người gửi tiết kiệm 100 triệu kỳ hạn 9 tháng với lãi suất 6,5% một năm. Biết lãi được tính hàng tháng, tiền lãi mỗi tháng không cộng dồn vào từng tháng để tính lãi cho các tháng tiếp theo mà chỉ được cộng dồn khi hết kỳ hạn gửi mà người đó không lĩnh tiền thì nó mới được cộng dồn và tự động gia hạn với kỳ hạn mới mà bạn đã đăng ký trước đó. Tính số tiền mà người đó nhận được sau 9 tháng.

A. 103,785 triệu đồng

B. 105,324 triệu đồng

C. 104,785 triệu đồng

D. 90,765 triệu đồng

Xem đáp án

Đáp án C

Số tiền người đó nhận được sau 9 tháng là

$100 + 100 .0, 065 .9 / 12$ $= 104, 875 (trieu) .$

Câu 43:

Tìm m để phương trình $4 {(\log_{3} \sqrt{x})}^{2} - \log_{\frac{1}{3}} x + m = 0$ có nghiệm thuộc khoảng $(0; 1)$ .

A. $m > \frac{1}{4}$

B. $m \leq \frac{1}{4}$

C. $0 \leq m \leq \frac{1}{4}$

D. $0 < m < \frac{1}{4}$

Xem đáp án

Để thỏa mãn đề bài thì (1) phải có nghiệm âm (có hai nghiệm âm, có một nghiệm âm) hay

Câu 44:

Gọi $z_{1}, z_{2}$ là nghiệm phức của phương trình $z^{2} + 2 z + 3 = 0 .$ Đặt $w = {(1 + z_{1})}^{100} + {(1 + z_{2})}^{100} .$ Khi đó

A. $- 2^{51} i$

B. $2^{51}$

C. $- 2^{51}$

D. $2^{51} i$

Xem đáp án

Câu 45:

Giá trị lớn nhất của hàm số $y = \frac{x^{2} + 2 x + 1}{x - 1}$ trên đoạn $[- 1; 2]$ là

A. 0

B. 9

C. Không tồn tại

D. 8

Xem đáp án

Dựa vào bảng biến thiên ta thấy, không tồn tại giá trị nhỏ nhất của hàm số trong đoạn $[- 1; 2]$

Câu 46:

07/07/2024

Tìm tất cả các giá trị của tham số m để ba điểm cực trị của đồ thị hàm số $y = x^{4} + (2 m - 2) x^{2} + 1 - m$ là ba đỉnh của một tam giác vuông

A. m = 0

B.

C. m = -1

D. m = 1

Xem đáp án

Câu 47:

Có bao nhiêu số $a \in (0; 10 π)$ sao cho $\int_{0}^{a} \sin^{3} x . \sin 2 xdx = \frac{2}{5} ?$

A. 4

B. 6

C. 10

D. 5

Xem đáp án

Câu 48:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $(P) : x - y + z + 3 = 0$ và ba điểm $A (0; 1; 2), B (1; 1; 1), C (2; - 2; 3) .$ Tọa độ điểm M thuộc (P) sao cho $|\vec{MA} + \vec{MB} + \vec{MC}|$ nhỏ nhất là

A. $M (- 1; 2; 0)$

B. $M (1; 1; - 3)$

C. $M (0; 0; - 3)$

D. $M (2; 1; - 1)$

Xem đáp án

Câu 49:

Tìm độ dài các cạnh góc vuông của tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số $a (a > 0) .$

A. $\frac{a}{3}; \frac{a \sqrt{3}}{3}$

B. $\frac{a}{2}; \frac{a}{2}$

C. $\frac{a}{3}; \frac{2 \sqrt{2} a}{3}$

D. $\frac{a}{5}; \sqrt{\frac{3}{5}} a$

Xem đáp án

Câu 50: