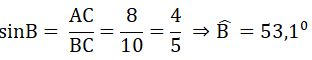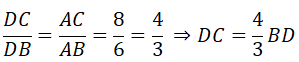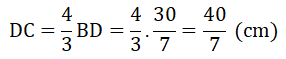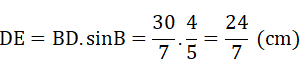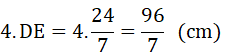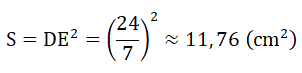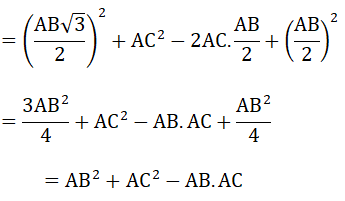12 câu hỏi trắc nghiệm thuộc Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án

Câu 1:

19/07/2024

Phần trắc nghiệm

Nội dung câu hỏi 1

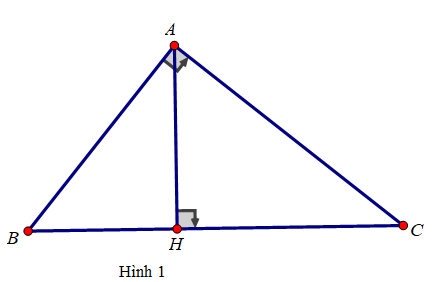
Dựa vào hình 1, hãy chọn câu đúng nhất:

A. $B A^{2}$ =BC.CH

B. $B A^{2}$ = BC.BH

C. $B A^{2} = B C^{2} + A C^{2}$

D.Cả 3 ý A,B,C đều sai

Xem đáp án

Đáp án là B

Câu 2:

19/07/2024

Dựa vào hình 1, độ dài của đoạn thẳng AH bằng

A.AB.AC

B.BC.HB

C. $\sqrt{H B . H C}$

D.BC.HC

Xem đáp án

Đáp án là C

Câu 3:

18/07/2024

Dựa vào hình 1, hệ thức nào sau đây là đúng:

A. $\cos C = \frac{A B}{A C}$

B. $\tan B = \frac{A B}{A C}$

C. $c o t g B = \frac{A C}{A B}$

D. $c o t g C = \frac{H C}{H A}$

Xem đáp án

Đáp án là D

Câu 4:

23/07/2024

Cho tam giác ABC vuông tại A có ∠B = $60^{0}$ , AB = 6 cm. Kẻ đường cao AH. Độ dài đường cao AH là:

A.3 cm

B.3 $\sqrt{3}$ cm

C.6 $\sqrt{3}$ cm

D.Một kết quả khác

Xem đáp án

Đáp án là B

Câu 5:

14/07/2024

Đẳng thức nào sau đây không đúng

A.sin $37^{0}$ = cos $53^{0}$

B.tan $30^{0}$ .cotg $30^{0}$ = 1

C. $\frac{\cos 18^{0}}{\cos 72^{0}} = c o t g 18^{0}$

D. $\sin α + \cos α = 1$

Xem đáp án

Đáp án là C

Câu 6:

22/07/2024

Giá trị của biểu thức: sin $59^{0}$ - cos $31^{0}$ bằng:

A.0

B.cos $28^{0}$

C.sin $28^{0}$

D.0,5

Xem đáp án

Đáp án là A

Câu 7:

23/07/2024

Phần tự luận

Nội dung câu hỏi 1

Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm

a) Tính BC, ∠B, ∠C

Xem đáp án

a) Xét tam giác ABC vuông tại A có:

$B C^{2} = A B^{2} + A C^{2} = 6^{2} + 8^{2}$ = 100

⇒ BC = 10 (cm)

∠B + ∠C = $90^{0}$ ⇒ ∠C = $90^{0} - 53, 1^{0}$ = $36, 9^{0}$

Câu 8:

23/07/2024

Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm

b) Phân giác của góc A cắt BC tại D. Tính BD, CD

Xem đáp án

b) Do AD là tia phân giác của góc BAC, D ∈ BC nên ta có:

Mặt khác ta lại có:

DC + DB = BC ⇒ (4/3.BD) + BD = 10 ⇒ 7/3.BD = 10 ⇒ BD = 30/7 (cm)

Khi đó:

Câu 9:

17/07/2024

Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm

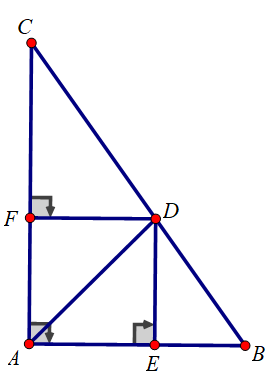
c) Từ D kẻ DE, DF vuông góc với AB, AC. Tứ giác AEDF là hình gì? Tính chu vi và diện tích của tứ giác AEDF

Xem đáp án

c) Xét tứ giác AEDF có:

∠(EAF) = ∠(AFD) = ∠(AED) = $90^{0}$

⇒ Tứ giác AEDF là hình chữ nhật

Lại có: ΔAFD vuông tại F, có ∠(FAD) = $45^{0}$

⇒ ΔAFD vuông cân tại F

⇒ AF = FD

⇒ tứ giác AEDF là hình vuông

Xét tam giác DEB vuông tại D có:

Chu vi hình vuông AEDF là:

Diện tích hình vuông AEDF là:

Câu 10:

16/12/2024

Cho α là góc nhọn, sinα = 1/2.Tính cosα;tanα;cotα

Xem đáp án

Lời giải

Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα

Ta có: $\sin^{2} α + \cos^{2} α = 1$

*Phương pháp giải:

Sử dụng công thức lượng giác cơ bản

$1 . \tan (x) = \frac{\sin (x)}{\cos (x)} 2 . c o t (x) = \frac{\cos (x)}{\sin (x)} 3 . \sin^{2} (x) + \cos^{2} (x) = 1 4 . \tan (x) . c o t (x) = 1 (x \neq k \frac{π}{2}, k \in Z) 5 . 1 + \tan^{2} (x) = \frac{1}{\cos^{2} (x)} (x \neq \frac{π}{2} + k π, k \in Z) 6 . 1 + \cot^{2} (x) = \frac{1}{\sin^{2} (x)} (x \neq kπ, k \in Z)$

*Lý thuyết:

1. Công thức lượng giác cơ bản

$1 . \tan (x) = \frac{\sin (x)}{\cos (x)} 2 . c o t (x) = \frac{\cos (x)}{\sin (x)} 3 . \sin^{2} (x) + \cos^{2} (x) = 1 4 . \tan (x) . c o t (x) = 1 (x \neq k \frac{π}{2}, k \in Z) 5 . 1 + \tan^{2} (x) = \frac{1}{\cos^{2} (x)} (x \neq \frac{π}{2} + k π, k \in Z) 6 . 1 + \cot^{2} (x) = \frac{1}{\sin^{2} (x)} (x \neq kπ, k \in Z)$

2. Công thức cộng lượng giác

$\cos (x + y) = \cos (x) \cos (y) - \sin (x) \sin (y) \cos (x - y) = \cos (x) \cos (y) + \sin (x) \sin (y) \sin (x + y) = \sin (x) \cos (y) + \sin (y) \cos (x) \sin (x - y) = \sin (x) \cos (y) - \sin (y) \cos (x) \tan (x + y) = \frac{\tan (x) + \tan (y)}{1 - \tan (x) \tan (y)} \tan (x - y) = \frac{\tan (x) - \tan (y)}{1 + \tan (x) \tan (y)}$

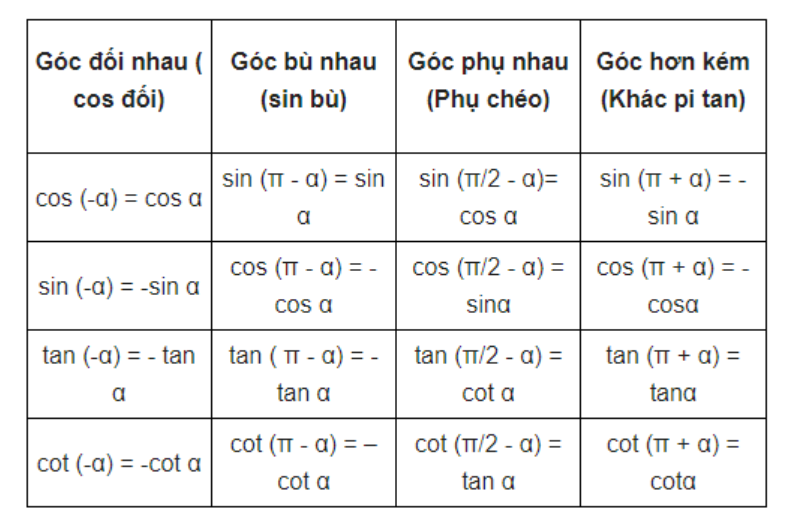
3. Công thức các cung liên kết trên đường tròn lượng giác

Mẹo nhớ: cos đối, sin bù, phụ chéo, tan hơn kém π

4. Công thức nhân

Công thức nhân đôi

$\cos^{2} (x) - \sin^{2} (x) = 2 \cos^{2} (x) - 1 = 1 - 2 \sin^{2} (x) \sin (2 x) = 2 \sin (x) \cos (x) \tan (2 x) = \frac{\tan (x)}{1 - \tan^{2} (x)}$

Công thức nhân ba

$\sin (3 x) = 3 \sin (x) - 4 \sin^{3} (x) \cos (3 x) = 4 \cos^{3} (x) - 3 \cos (x)$

Công thức nhân bốn

$8 \cos^{4} (a) - 8 \cos^{2} (a) + 1 = 8 \sin^{4} (a) - 8 \sin^{2} (a) + 1$

5. Công thức hạ bậc

Thực ra những công thức này đều được biến đổi ra từ công thức lượng giác cơ bản

Ví dụ như: sin²a=1 - cos²a = 1 - $\frac{\cos (2 a) + 1}{2}$ = $\frac{1 - \cos (2 a)}{2}$ .

$\frac{1 - \cos (2 x)}{2} \tan^{2} (x) = \frac{1 - \cos (2 x)}{1 + \cos (2 x)}$

6. Công thức biến đổi tổng thành tích

$1 . \cos (a) + \cos (b) = 2 \cos (\frac{a + b}{2}) . \cos (\frac{a - b}{2}) 2 . \cos (a) - \cos (b) = - 2 \sin (\frac{a + b}{2}) . \sin (\frac{a - b}{2}) 3 . \sin (a) + \sin (b) = 2 \sin (\frac{a + b}{2}) . \cos (\frac{a - b}{2}) 4 . \sin (a) - \sin (b) = 2 \cos (\frac{a + b}{2}) . \sin (\frac{a - b}{2}) 5 . \tan (a) + \tan (b) = \frac{\sin (a + b)}{\cos (a) . \cos (b)} 6 . \tan (a) - \tan (b) = \frac{\sin (a - b)}{\cos (a) . \cos (b)} 7 . \sin (a) + \cos (a) = \sqrt{2} \sin (a + \frac{π}{4}) = \sqrt{2} \cos (a - \frac{π}{4}) 8 . \sin (a) - \cos (a) = \sqrt{2} \sin (a - \frac{π}{4}) = - \sqrt{2} \cos (a + \frac{π}{4}) 9 . \tan (a) + c o t (a) = \frac{2}{\sin (2 a)} 10 . c o t (a) - \tan (a) = 2 c o t (2 a) 11 . \sin^{4} (a) + \cos^{4} (a) = 1 - \frac{1}{2} \sin^{2} (2 a) = \frac{1}{4} \cos (4 a) + \frac{3}{4} 12 . \sin^{6} (a) + \cos^{6} (a) = 1 - \frac{3}{4} \sin^{2} (2 a) = \frac{3}{8} \cos (4 a) + \frac{5}{8}$

Xem thêm

Tổng hợp bảng giá trị lượng giác (2024) đầy đủ, chi tiết nhất

TOP 12 câu Trắc nghiệm Công thức lượng giác (Kết nối tri thức 2024) có đáp án - Toán 11

Câu 11:

21/07/2024

Cho α là góc nhọn, chứng minh rằng:

$\frac{1 - \tan α}{1 + \tan α} = \frac{\cos α - \sin α}{\cos α + \sin α}$

Xem đáp án

Câu 12:

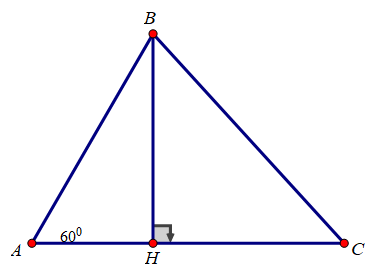
20/07/2024

Cho tam giác ABC có ∠A = $60^{0}$ Chứng minh rằng:

$B C^{2} = A B^{2} + A C^{2}$ - AB.AC

Xem đáp án

Kẻ đường cao BH

Xét tam giác ABH vuông tại H có ∠(BAC) = $60^{0}$

BH = AB.sin A = AB.sin $60^{0}$ = (AB $\sqrt{3}$ )/2

AH = AB.cos A = AB.cos $60^{0}$ = AB/2

Xét tam giác BHC vuông tại H có:

$B C^{2} = B H^{2} + H C^{2} = B H^{2} + {(A C - A H)}^{2}$

= $B H^{2} + A C^{2} - 2 A C . A H + A H^{2}$

Vậy được điều phải chứng minh.

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3