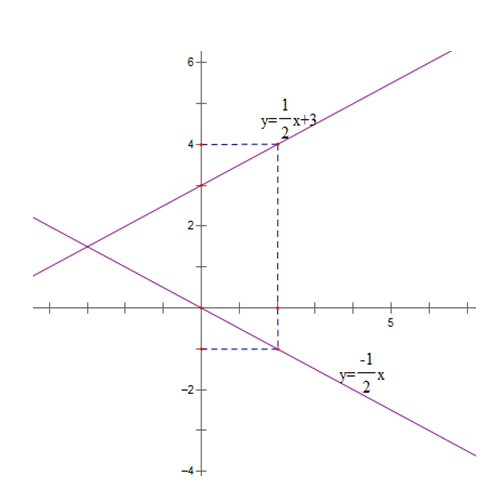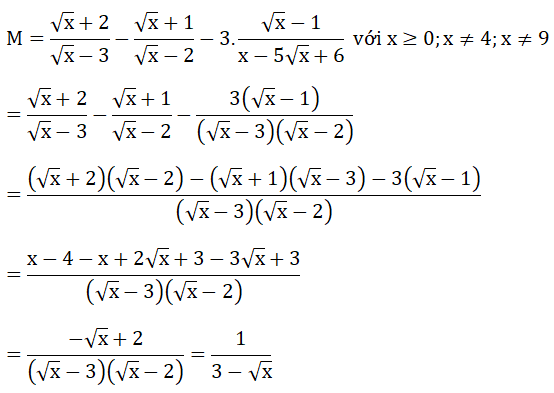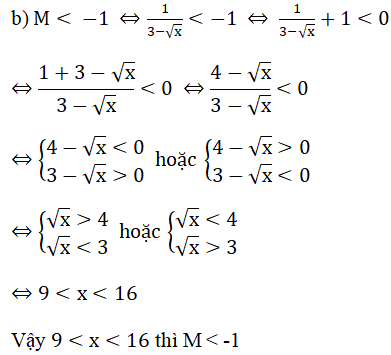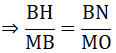Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án
-
4303 lượt thi
-
12 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 4:
11/07/2024a) Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau:
Xem đáp án
a) Tập xác định của hàm số R
Bảng giá trị
| x | 0 | 2 |
| y = -1/2 x | 0 | - 1 |
| y = 1/2 x + 3 | 3 | 4 |
Câu 5:
22/07/2024Xác định b để đường thẳng () y = 2x + b cắt ( ) tại điểm có hoành độ và tung độ đối nhau.
Xem đáp án
b) Gọi A (m; - m) là tọa độ giao điểm của () và ()
Khi đó:
-m = 1/2 m + 3 ⇔ 3/2 m = 3 ⇔ m = 2
Vậy tọa độ giao điểm của và là (2; -2)
⇒ -2 = 2.2 + b ⇔ b = -6
Vậy b = - 6
Câu 9:
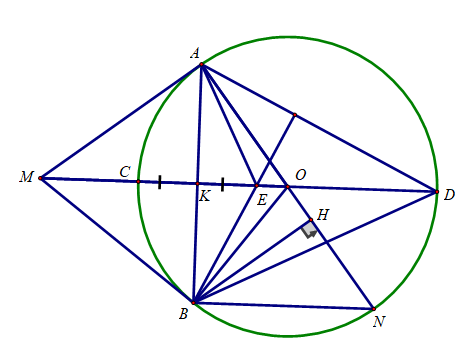
23/07/2024Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
a) Chứng minh K là trung điểm của AB.
Xem đáp án
a) Ta có:
MA = MB ( tính chất 2 tiếp tuyến cắt nhau)
OA = OB ( cùng bằng bán kính đường tròn (O)
⇒ OM là đường trung trực của AB
OM ∩ AB = K ⇒ K là trung điểm của AB
Câu 10:
23/07/2024Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
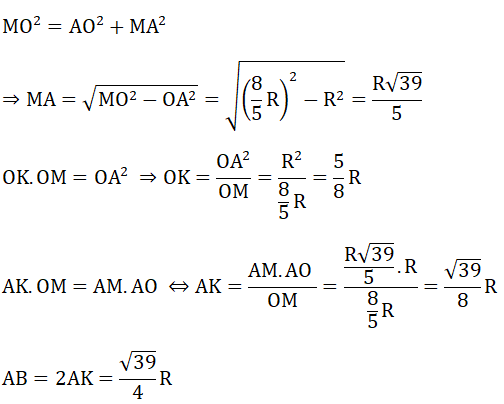
b) Tính MA, AB, OK theo R.
Xem đáp án
b) Tam giác MAO vuông tại A, AK là đường cao có:
Câu 11:
20/07/2024Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN = BH.MO .
Xem đáp án
c) Ta có: ∠(ABN ) = (B thuộc đường tròn đường kính AN)
⇒ BN // MO ( cùng vuông góc với AB)
Do đó:
∠(AOM) = ∠(ANB) (đồng vị))
∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))
⇒ ∠(ANB) = ∠(BOM)
Xét ΔBHN và ΔMBO có:
∠(BHN) = ∠(MBO ) =
∠(ANB) = ∠(BOM)
⇒ ΔBHN ∼ ΔMBO (g.g)
Hay MB. BN = BH. MO
Câu 12:
23/07/2024Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
d) Đường thẳng MO cắt đường tròn (O) tại C và D (C nằm giữa O và M). Gọi E là điểm đối xứng của C qua K. Chứng minh E là trực tâm của tam giác ABD.
Xem đáp án
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB