299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết
299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết (P1) (Đề 7)
-
1541 lượt thi
-
40 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 3:
13/07/2024Anh Bảo gửi 27 triệu đồng vào ngân hàng theo thể thức lãi kép, kỳ hạn là một quý, với lãi suất 1,85% một quý. Hỏi thời gian tối thiểu bao nhiêu để anh Bảo có được ít nhất 36 triệu đồng tính cả vỗn lẫn lãi?
 Xem đáp án
Xem đáp án
Chọn A
Câu 4:
21/07/2024Ông A vay ngân hàng 50 triệu đồng với lãi suất 0,67% /tháng. Ông ta muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông ta bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ mỗi tháng đều bằng nhau và bằng 3 triệu. Biết rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi bằng cách hoàn nợ đó, ông A cần trả ít nhất bao nhiêu tháng kể từ ngày vay đến lúc trả hết nợ ngân hàng (giả định trong thời gian này lãi suất không thay đổi)
 Xem đáp án
Xem đáp án
Chọn C
Câu 5:
16/07/2024Một người vay ngân hàng số tiền 400 triệu đồng, mỗi tháng trả góp 10 triệu đồng và lãi suất cho số tiền chưa trả là 1% mỗi tháng. Kỳ trả đầu tiên là cuối tháng thứ nhất. Biết lãi suất không đổi trong suốt quá trình gửi, hỏi số tiền còn phải trả ở kỳ cuối là bao nhiêu để người này hết nợ ngân hàng? (làm tròn đến hàng nghìn).
 Xem đáp án
Xem đáp án
Chọn B
Câu 6:
14/07/2024Mỗi tháng bà A gửi vào ngân hàng một khoản tiền không đổi với lãi suất cố định là 0,4% 1 tháng. Ba năm rưỡi kể từ ngày gửi khoản tiền đầu tiên, bà A rút toàn bộ số tiền để mua xe. Số tiền nhận về lấy đến hàng nghìn là 91.635.000. Hỏi khoản tiền gửi mỗi tháng của bà A là bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn A
Câu 7:
21/07/2024Tập hợp các số thực m để phương trình có nghiệm thực là
 Xem đáp án
Xem đáp án
Chọn D vì hàm số
Câu 10:
21/07/2024Cho hàm số liên tục trên R và có đồ thị như hình bên dưới
Biết rằng trục hoành là tiệm cận ngang của đồ thị. Tìm tất cả các giá trị thực của tham số m để phương trình có hai nghiệm dương phân biệt
 Xem đáp án
Xem đáp án
Chọn D
Từ đồ thị ta thấy thì
Câu 12:
05/12/2024Phương trình có bao nhiêu nghiệm âm
 Xem đáp án
Xem đáp án
Đáp án đúng là C
*Lời giải
*Phương pháp giải:
- Đưa phương trình mũ về dạng ẩn phụ quen thuộc;
- Đặt ẩn phụ thích hợp và tìm điều kiện cho ẩn phụ;
- Giải phương trình mũ với ẩn phụ mới và tìm nghiệm thỏa mãn;
- Thay giá trị vừa tìm được vào phương trình mũ;
Kết luận
*Lý thuyết:
1. Phương trình mũ cơ bản
– Phương trình mũ cơ bản có dạng: ax = b (a > 0; a ≠ 1).
Để giải phương trình trên, ta sử dụng định nghĩa logarit.
Với b > 0 ta có: ax = bx = logab.
Với b ≤ 0, phương trình vô nghiệm.
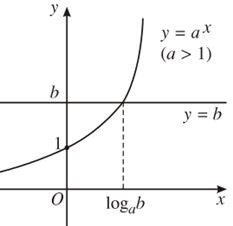
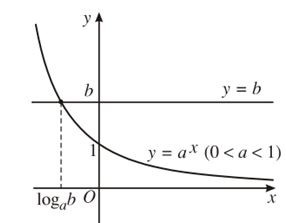
– Minh họa bằng đồ thị
Hoành độ giao điểm của đồ thị hai hàm số y = ax và y = b là nghiệm của phương trình ax = b.
Số nghiệm của phương trình là số giao điểm của hai đồ thị.
Rõ ràng, nếu b ≤ 0 thì hai đồ thị không cắt nhau nên phương trình vô nghiệm.
Nếu b > 0 ta có hai đồ thị như hình dưới đây. Trên mỗi hình, hai đồ thị luôn cắt nhau tại một điểm nên phương trình có nghiệm duy nhất.
Xem các bài viết liên quan hay, chi tiết:
Lý thuyết Toán 12 Bài 5: Phương trình mũ và phương trình logarit
Phương trình mũ và cách giải các dạng bài tập
Câu 13:
19/07/2024Biết phương trình có nghiệm duy nhất trong đó a;b là những số nguyên. Khi đó bằng
 Xem đáp án
Xem đáp án
Chọn A
Bài thi liên quan
-
299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết (P1) (Đề 1)
-
40 câu hỏi
-
50 phút
-
-
299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết (P1) (Đề 2)
-
40 câu hỏi
-
50 phút
-
-
299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết (P1) (Đề 3)
-
40 câu hỏi
-
50 phút
-
-
299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết (P1) (Đề 4)
-
40 câu hỏi
-
50 phút
-
-
299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết (P1) (Đề 5)
-
40 câu hỏi
-
50 phút
-
-
299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết (P1) (Đề 6)
-
40 câu hỏi
-
50 phút
-
-
299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết (P1) (Đề 8)
-
19 câu hỏi
-
50 phút
-
