(2023) Đề thi thử Toán THPT Liên Trường Nghệ An có đáp án
(2023) Đề thi thử Toán THPT Liên Trường Nghệ An có đáp án
-
550 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 2:
20/07/2024 Xem đáp án
Xem đáp án
Chọn B
Tập xác định: .
Ta có là đường tiệm cận đứngCâu 3:
21/07/2024 Xem đáp án
Xem đáp án
Chọn D
Ta có .
Bảng xét dấu f'(x):

Vậy hàm số có hai điểm cực trị.
Câu 4:
22/07/2024Cho hàm số y = f(x) xác định trên R và có bảng xét dấu đạo hàm như sau:

Khi đó hàm số y = f(x) đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Chọn C
Từ bảng xét dấu, hàm số y = f(x) đồng biến trên khoảng (-1;2)Câu 5:
22/07/2024 Xem đáp án
Xem đáp án
Chọn B
Câu 8:
20/07/2024 Xem đáp án
Xem đáp án
Chọn C
Ta có . Do đó hàm số đồng biến trên [1;2].
Khi đóCâu 9:
20/07/2024 Xem đáp án
Xem đáp án
Chọn A
Điều kiện .
Tập xác định của hàm số làCâu 10:
23/07/2024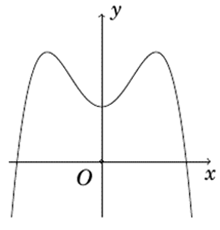
 Xem đáp án
Xem đáp án
Chọn A
Đồ thị của hàm số có dạng của hàm số nên loại phương án B và. D.
Lại có nên a < 0, do đó loại phương án. C.Câu 11:
20/07/2024 Xem đáp án
Xem đáp án
Chọn B
Ta cóCâu 14:
22/07/2024 Xem đáp án
Xem đáp án
Chọn C
Ta cóCâu 15:
21/07/2024 Xem đáp án
Xem đáp án
Chọn B
Công sai của cấp số cộng đã cho làCâu 17:
22/07/2024 Xem đáp án
Xem đáp án
Chọn D
Câu 18:
22/07/2024 Xem đáp án
Xem đáp án
Chọn C
Hình chóp có đáy là đa giác có đường tròn ngoại tiếp thì có mặt cầu ngoại tiếp.
Câu 19:
23/07/2024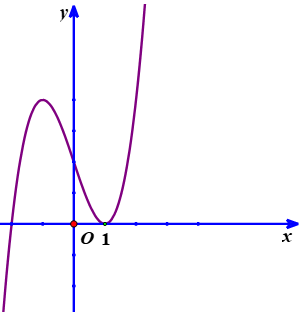
 Xem đáp án
Xem đáp án
Chọn D
Từ đồ thị hàm số ta có bảng xét dấu của y = f'(x).
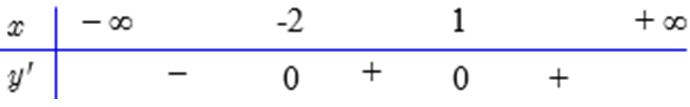
Do đó hàm số y = f(x) có 1 cực trị.
Câu 20:
22/07/2024 Xem đáp án
Xem đáp án
Chọn C
Thể tích khối chóp mới làCâu 22:
22/07/2024 Xem đáp án
Xem đáp án
Chọn C
Điều kiện x > 0.
Ta có
So với điều kiện ta có .
Suy ra nghiệm nguyên của bất phương trình đã cho là x = 1.
Vậy bất phương trình có 1 nghiệm nguyên.
Câu 23:
04/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Lời giải:
Thể tích của khối trụ là suy ra* Các lý thuyết thêm về mặt trụ, mặt cầu và mặt nón:
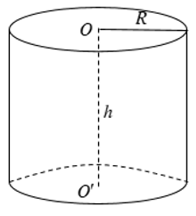
1. Diện tích và thể tích hình trụ
Cho hình trụ có bán kính đáy R và chiều cao h.
- Diện tích xung quanh: Sxq = 2πRh.
- Diện tích toàn phần: Stp = 2πRh + 2πR2.
- Thể tích: V = πR2h.
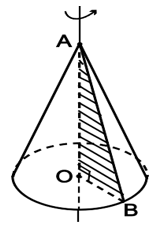
2. Diện tích và thể tích của hình nón
Đặt AC = l; l là đường sinh.
Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.
- Diện tích xung quanh: Sxq = πRl.
- Diện tích toàn phần: Stp = πRl + πR2.
- Thể tích: V=13πR2h.
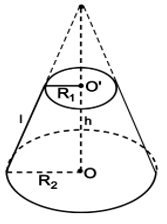
3. Diện tích và thể tích hình nón cụt
Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.
- Diện tích xung quanh: Sxq = π (R + r) l.
- Thể tích: V=13πh(R2+Rr+r2).
Câu 24:
22/07/2024 Xem đáp án
Xem đáp án
Chọn D
Thể tích khối chóp S.ABCD làCâu 25:
23/07/2024 Xem đáp án
Xem đáp án
Chọn C
Gọi là tâm mặt cầu (S).
Mặt cầu đi qua hai điểm A(-1;-2;4), B(2;1;2) nên
.
Bán kính của mặt cầu làCâu 26:
05/11/2024Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ A đến mặt phẳng (BDD'B') bằng
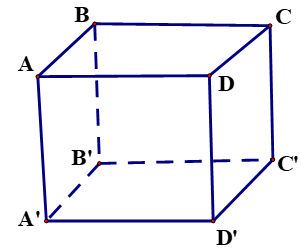
 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Lời giải:
Gọi O là giao điểm của AC và BD.
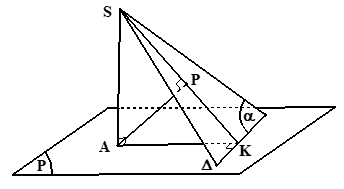
Ta cóĐể tính được khoảng từ điểm A đến mặt phẳng (α) thì điều quan trọng nhất là ta phải xác định được hình chiếu của điểm A trên (α)
Cho trước SA ⊥ Δ; trong đó S ∈ (α) và Δ ⊂ (α)
Bước 1: Dựng AK ⊥ Δ ⇒ Δ ⊥ (SAK) ⇒(α) ⊥ (SAK) và (α) ∩ (SAK) = SK
Bước 2: Dựng AP ⊥ SK ⇒ AP ⊥ (α) ⇒ d(A, (α)) = AP
Lý thuyết khoảng cách từ một điểm đến một mặt phẳng
- Khoảng cách từ điểm M đến mặt phẳng (P) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên mặt phẳng (P).
- Kí hiệu: d (M, (P)) = MH
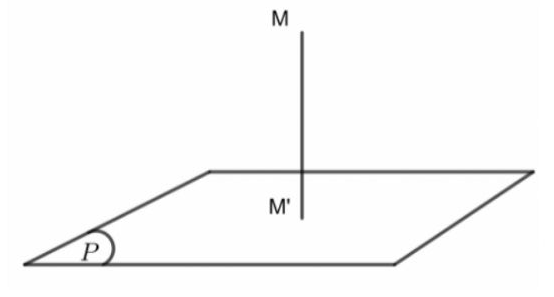
Công thức tính khoảng cách từ một điểm đến mặt phẳng
Cho hệ tọa độ không gian Oxyz, cho điểm M có tọa độ như sau: (α;β;γ). Cho mặt phẳng (P) có phương trình dạng: ax + by + cz + d = 0.
Công thức tổng quát tính khoảng cách từ điểm M đến mặt phẳng (P) được tính như sau:
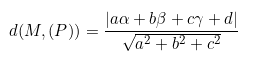
Cách tính khoảng cách từ một điểm đến một mặt phẳng
Để tính được khoảng từ điểm A đến mặt phẳng (α) thì điều quan trọng nhất là ta phải xác định được hình chiếu của điểm A trên (α)
Cho trước SA ⊥ Δ; trong đó S ∈ (α) và Δ ⊂ (α)
Bước 1: Dựng AK ⊥ Δ ⇒ Δ ⊥ (SAK) ⇒(α) ⊥ (SAK) và (α) ∩ (SAK) = SK
Bước 2: Dựng AP ⊥ SK ⇒ AP ⊥ (α) ⇒ d(A, (α)) = AP
1. Khoảng cách từ một điểm đến mặt phẳng.
Phương pháp giải:
Khoảng cách từ M(x0;y0;z0) đến mặt phẳng (P): Ax + By + Cz + D = 0 là:
d(M,(P))=|Ax0+By0+Cz0+D|√A2+B2+C2.
2. Khoảng cách giữa hai mặt phẳng song song.
Phương pháp giải:
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm thuộc mặt phẳng này đến mặt phẳng kia. Cụ thể, để tính khoảng cách giữa hai mặt phẳng song song (P) và (Q) ta thực hiện các bước như sau:
+) Lấy điểm M thuộc mặt phẳng (P).
+) Tính khoảng cách từ điểm M đến mặt phẳng (Q) (áp dụng công thức khoảng cách từ một điểm đến mặt phẳng).
3. Khoảng cách từ một điểm đến một đường thẳng
Phương pháp giải:
Khoảng cách từ điểm M đến một đường thẳng d đi qua điểm A có vectơ chỉ phương →u được xác định bởi công thức:
d⎛⎜⎝M,d⎞⎟⎠=∣∣∣[−−→AM;→u]∣∣∣∣∣→u∣∣.
4. Khoảng cách giữa hai đường thẳng song song
Phương pháp giải:
Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm thuộc đường thẳng này đến đường thẳng kia. Cụ thể, để tính khoảng cách giữa hai đường thẳng song song d và d’ ta thực hiện như sau:
+) Lấy M thuộc đường thẳng d.
+) Tính khoảng cách từ M đến đường thẳng d’ (bằng công thức khoảng cách từ một điểm đến một đường thẳng).
Câu 27:
22/07/2024 Xem đáp án
Xem đáp án
Chọn C
Câu 28:
21/07/2024Chọn khẳng định sai trong các khẳng định sau:
Trong một khối đa diện Xem đáp án
Xem đáp án
Chọn D
Câu 29:
20/07/2024 Xem đáp án
Xem đáp án
Chọn A
Điều kiện .
là tiệm cận ngang.
là tiệm cận đứng.
Câu 31:
22/07/2024Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên dưới.
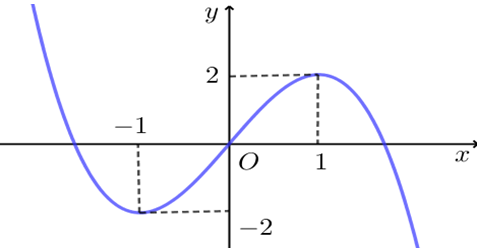
 Xem đáp án
Xem đáp án
Chọn B
Phương trình f(x) = 1 có ba nghiệm phân biệt.Câu 32:
22/07/2024 Xem đáp án
Xem đáp án
Chọn B
Để thoả mãn yêu cầu bài toán thìCâu 33:
23/07/2024 Xem đáp án
Xem đáp án
Chọn C
Ta có , ta có .
Mặt khác: .
Khi đó . Do nên m - 2 = 3 <=> m = 5
Vậy -10 < m < 6Câu 34:
22/07/2024 Xem đáp án
Xem đáp án
Chọn C
Ta có
.
Vậy tổng các nghiệm là:Câu 35:
20/07/2024 Xem đáp án
Xem đáp án
Chọn B
Ta có .
Vậy hàm số nghịch biên trên khoảng (-1;1)Câu 36:
23/07/2024 Xem đáp án
Xem đáp án
Chọn C
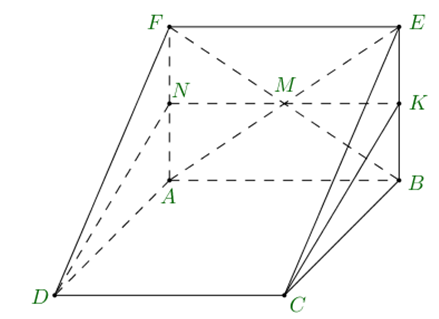
Gọi N, K lần lượt là trung điểm của AF, BE. Khi đó (MCD) là (NKCD).
Do
Suy ra .
Đặt AB= a (a > 0). Tam giác NDF có: .
Suy ra:Câu 37:
22/07/2024 Xem đáp án
Xem đáp án
Chọn B
Điều kiện:
Đặt ;
Thay t vào (2) ta được: .
Phương trình (1) có hai nghiệm thỏa mãn
<=> (3) có hai nghiệm phân biệt thỏa mãn
, với
Câu 38:
22/07/2024 Xem đáp án
Xem đáp án
Chọn A
- Số cách chọn ngẫu nhiên 4 gian hàng trong 15 gian hàng đã cho là: .
- Gọi A là biến cố: “trong 4 gian hàng chọn được của doanh nghiệp X có đúng 3 gian hàng kề nhau”. Ta tính n(A):
- TH1: Ba gian hàng kề nhau ở đầu dãy hoặc cuối dãy: Khi đó, chọn ba gian hàng kề nhau có 2 cách, gian hàng còn lại có 11 cách chọn. Suy ra, có 2.11 = 22 cách chọn.
- TH2: Ba gian hàng kề nhau, không có gian hàng nào nằm ở đầu dãy hoặc cuối dãy: Khi đó, có 11 cách chọn ba gian hàng kề nhau. Gian hàng thứ tư được chọn phải khác 5 gian hàng(gồm 3 gian hàng kề nhau đã chọn và 2 gian hàng kề ba gian hàng đó), nên có 10 cách chọn gian hàng thứ tư. Suy ra, có 11.10 = 110 cách chọn.
Vậy . Suy ra:Câu 39:
22/07/2024 Xem đáp án
Xem đáp án
Chọn B
Đặt . Do:
Mà nên hàm số f(x) có hai điểm cực trị.
Để hàm số có nhiều điểm cực trị nhất thì phương trình f(x) = 0 có ba nghiệm phân biệt.
Khảo sát hàm số f(x) = 0 ta vẽ được được hình ảnh đồ thị hàm số như sau:
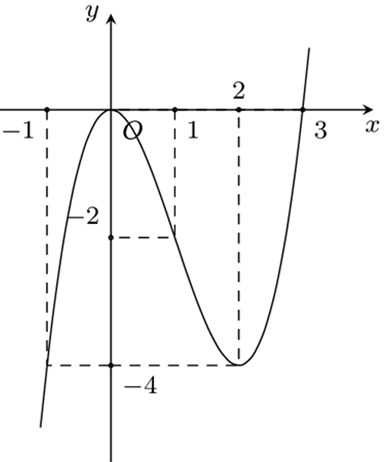
Nên phương trình có nhiều nghiệm bội lẻ nhất khi: .
Vậy có 3 giá trị nguyên của tham số m để hàm số có nhiều điểm cực trị nhất.
Câu 40:
22/07/2024Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên dưới.
![Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên dưới. Số nghiệm thực phân biệt của phương trình f[f(x) + 1] + 2 = 0 là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid2-1683044394.png)
Số nghiệm thực phân biệt của phương trình là
 Xem đáp án
Xem đáp án
Chọn C
Ta có:
Thì phương trình có 3 nghiệm phân biệt.
với a < -1 thì phương trình có ![]() nghiệm.
nghiệm.
Vậy phương trình: có 4 nghiệm thực phân biệt.
Câu 41:
23/07/2024 Xem đáp án
Xem đáp án
Chọn D

Suy ra .
Gọi H là hình chiếu của A' trên AD. Có nên .
Suy ra .
Có .
Câu 42:
22/07/2024Cho hàm số bậc ba y = f(x). Hàm số g(x) = f(x + 2) có bảng biến thiên như bên dưới.
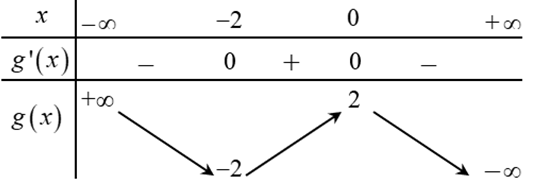
 Xem đáp án
Xem đáp án
Chọn C
Từ gt tìm được có BBT
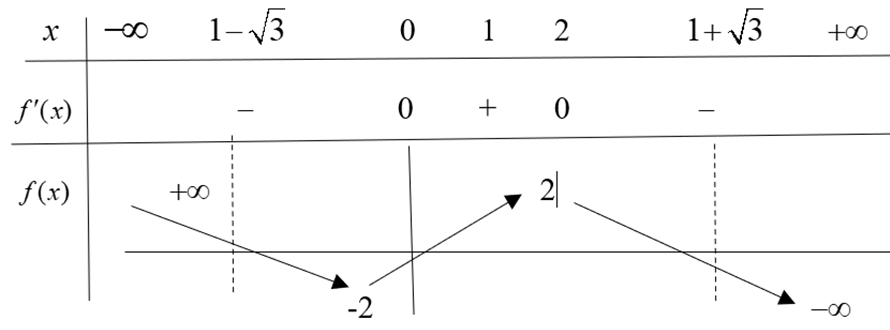
Phương trình , Đk
TH1:
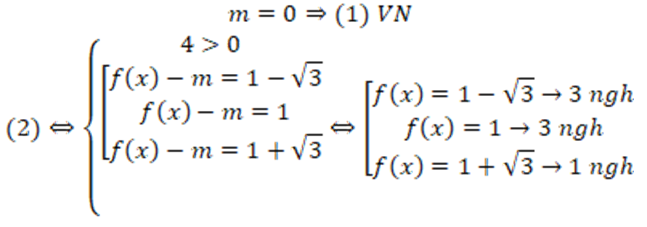
TH2:
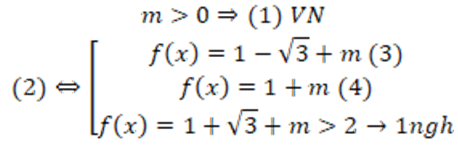
Yêu cầu bài toán
TH3: 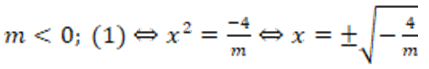
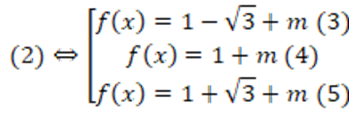
![]()
Yêu cầu bài toán ó <=> (2) có đúng 3 nghiệm phân biệt
Nếu không có số nguyên nào thỏa mãn
Nếu (3), (4), (5), mỗi pt 1 nghiệm và nghiệm > 3( không thỏa mãn)
Nên có các giá trị m nguyên là
+) có 1 nghiệm > 3( không tm)
(4) <=> f(x) = -3 -> 1 nghiệm > 3 (KTM)
có 3 nghiệm pb trong đó có 1 nghiệm > 2 (KTM)
+) m = -3
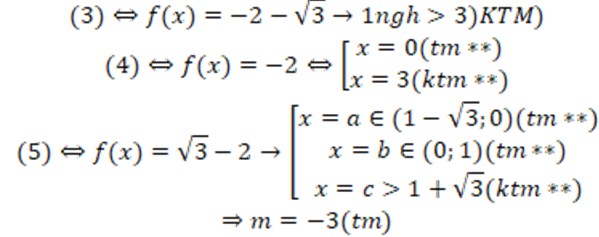
+) m = -2
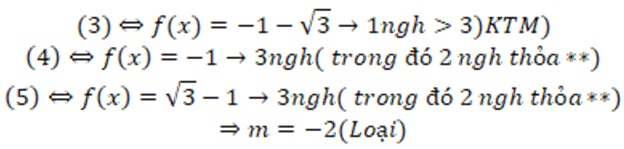
+) m = -1
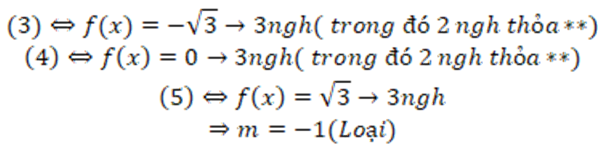
Vậy m = 2 hoặc m = -3, nên tổng các giá trị của m bằng -1, chọn đáp án C.
Câu 43:
22/07/2024Cho hai khối cầu có tổng diện tích bằng tiếp xúc ngoài nhau và cùng tiếp xúc với mặt phẳng (P) lần lượt tại hai điểm A, B. Tính tổng thể tích của hai khối cầu đó biết .
 Xem đáp án
Xem đáp án
Chọn C
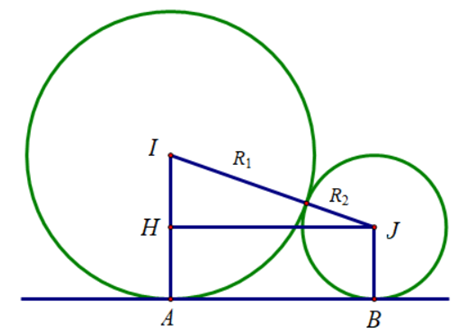
Gọi là bán kính ; I, J là tâm của các mặt cầu (như hình vẽ).
Gọi H là hình chiếu của J lên IA.
Theo bài ra, ta có hệ:
Câu 44:
22/07/2024Trong mặt phẳng (P) cho tam giác ABC có AB = 1, AC = 2, . Điểm S thay đổi thuộc đường thẳng đi qua A và vuông góc với (P), (S khác A). Gọi B1, C1 lần lượt là hình chiếu vuông góc của A trên SB, SC. Đường kính MN thay đổi của mặt cầu (T) ngoại tiếp khối đa diện ABCB1C1 và I là điểm cách tâm mặt cầu (T) một khoảng bằng ba lần bán kính. Tính giá trị nhỏ nhất của IM + IN.
 Xem đáp án
Xem đáp án
Chọn C
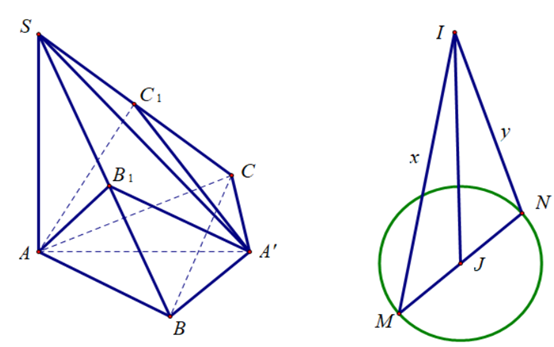
Ta có .
Bán kính đường tròn ngoại tiếp tam giác ABC: .
Gọi J là tâm đường tròn ngoại tiếp tam giác ABC, A' là điểm đối xứng của A qua J.
Ta dễ dàng chứng minh được: đều thuộc mặt cầu tâm J, đường kính .
Đặt .
+ Nếu I, J, M, N thẳng hàng thì .
+ Nếu I, J, M, N không thẳng hàng thì
.
Vậy, ta luôn có: .
Do .
.
Vậy .
Câu 45:
22/07/2024Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi là mặt phẳng đi qua CD’ và tạo với mặt phẳng (A'B'C'D') một góc với . Mặt phẳng chia khối lặp phương thành hai khối đa diện có thể tích là với . Tính V1.
 Xem đáp án
Xem đáp án
Chọn D
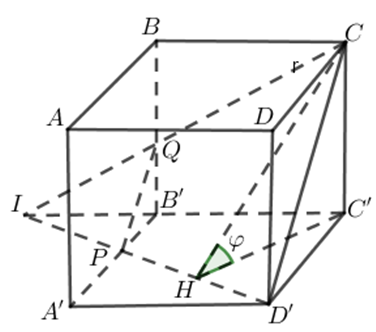
Mặt phẳng là mặt phẳng đi qua CD’ và cắt C'B' tại I .
Kẻ .
Ta có vuông tại .
Ta có vuông tại .
Ta thấy với C'I = 2a thì nên Q là trung điểm BB'.
nên P là trung điểm A'B'.
Ta có:
Vì .
Vậy .
Câu 46:
20/07/2024 Xem đáp án
Xem đáp án
Chọn B
Ta có .
Lấy tích phân hai vế cận chạy từ ta được:
.Câu 47:
22/07/2024Có bao nhiêu giá trị nguyên của tham số sao cho hàm số luôn đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Chọn D
.
Đặt
vì
Để hàm số đồng biến trên khoảng điều kiện là
Đặt
Để (1) nghiệm đúng với
.
Do
Vậy có 19 giá trị của m.
Câu 48:
22/07/2024Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;100] để bất phương trình nghiệm đúng với ?
 Xem đáp án
Xem đáp án
Chọn B
+ Giải (1)
Để (1) nghiệm đúng với . Do m nguyên thuộc đoạn [0;100] nên có 100 - 8 = 92 giá trị của m.
+ Giải (2)
Để (1) nghiệm đúng với không có giá trị nào của m thỏa mãn.
Vậy có 92 giá trị của m.
Câu 49:
22/07/2024 Xem đáp án
Xem đáp án
Chọn B
Ta có
Đặt t = xln10, khi đó
Với y > t,
Với y < t,
Với y = t, ta có
Xét hàm số , ta có
Bảng biến thiên:
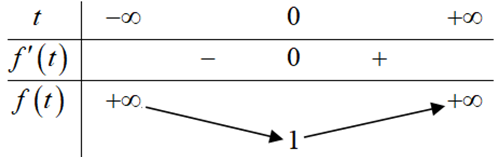
Từ bảng biến thiên ta thấy được
Đẳng thức xảy ra khi y = t = 0 hay x = y = 0.
Câu 50:
17/07/2024Trong hệ trục tọa độ Oxyz cho 3 điểm A(5;-2;0), B(4;5;-2) và C(0;3;2). Điểm M di chuyển trên trục Ox. Đặt . Biết giá trị nhỏ nhất của Q có dạng trong đó và b là số nguyên tố. Tính a + b.
 Xem đáp án
Xem đáp án
Chọn C
Ta có
Với G(3;2;0) là trọng tâm của tam giác ABC và I(2;4;0) là trung điểm BC, ta có:
,
Do G và I nằm cùng phía so với Ox nên gọi G'(3;-2;0) là điểm đối xứng của G qua Ox.
Khi đó .
Đẳng thức xảy ra khi M là giao điểm của G'I và Ox.
Có thể bạn quan tâm
- (2023) Đề thi thử Toán THPT Lý Thái Tổ, Bắc Ninh (Lần 1) có đáp án (590 lượt thi)
- (2023) Đề thi thử Toán THPT Chuyên Thái Bình (Lần 1) có đáp án (509 lượt thi)
- (2023) Đề thi thử Toán THPT Chuyên Khoa Học Tự Nhiên (Lần 1) có đáp án (484 lượt thi)
- (2023) Đề thi thử Toán THPT Chuyên Thái Bình (Lần 2) có đáp án (632 lượt thi)
- (2023) Đề thi thử Toán THPT Chuyên Hạ Long có đáp án (412 lượt thi)
- (2023) Đề thi thử Toán THPT Chuyên Lam Sơn có đáp án (436 lượt thi)
- (2023) Đề thi thử Toán THPT Liên Trường Nghệ An có đáp án (549 lượt thi)
- (2023) Đề thi thử Toán THPT Chuyên Hùng Vương có đáp án (679 lượt thi)