Câu hỏi:
21/07/2024 159
Cho cấp số cộng (un) có u1 = -2 và u2 = 1. Tìm công sai d.
A. d = -1
B. d = 3
C. d = 2
D. d = -3
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B
Công sai của cấp số cộng đã cho là
Chọn B
Công sai của cấp số cộng đã cho làCÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ A đến mặt phẳng (BDD'B') bằng
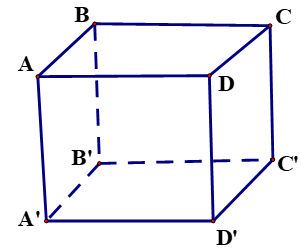
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ A đến mặt phẳng (BDD'B') bằng

Câu 2:
Trong không gian với hệ tọa độ Oxyz, gọi (S) là mặt cầu đi qua hai điểm A(-1;-2;4), B(2;1;2) và có tâm thuộc trục Oz. Bán kính của mặt cầu (S) là
Câu 3:
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật với AB = 2a, BC = a. Biết và Thể tích khối hộp ABCD.A'B'C'D' bằng
Câu 5:
Cho khối chóp tứ giác có đáy là hình vuông và có thể tích V. Nếu tăng độ dài chiều cao của khối chóp đã cho lên gấp ba và giữ nguyên cạnh đáy của nó thì ta được khối chóp mới có thể tích bằng
Câu 6:
Cho hàm số (m là tham số thực), thỏa mãn Mệnh đề nào dưới đây đúng?
Câu 7:
Trong hệ trục tọa độ Oxyz cho 3 điểm A(5;-2;0), B(4;5;-2) và C(0;3;2). Điểm M di chuyển trên trục Ox. Đặt . Biết giá trị nhỏ nhất của Q có dạng trong đó và b là số nguyên tố. Tính a + b.
Câu 8:
Hình chóp S.ABCD có diện tích đáy ABCD bằng a2 và độ dài đường cao bằng 6a. Thể tích khối chóp S.ABCD bằng
Câu 9:
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;100] để bất phương trình nghiệm đúng với ?
Câu 10:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi là mặt phẳng đi qua CD’ và tạo với mặt phẳng (A'B'C'D') một góc với . Mặt phẳng chia khối lặp phương thành hai khối đa diện có thể tích là với . Tính V1.
Câu 12:
Cho khối trụ có chiều cao h bằng bán kính đáy và thể tích . Tính chiều cao h của khối trụ đó.
Câu 13:
Cho hai khối cầu có tổng diện tích bằng tiếp xúc ngoài nhau và cùng tiếp xúc với mặt phẳng (P) lần lượt tại hai điểm A, B. Tính tổng thể tích của hai khối cầu đó biết .
Câu 14:
Cho hai hình vuông ABCD, ABEF nằm trong hai mặt phẳng vuông góc với nhau. M là tâm của hình vuông ABEF. Cosin góc giữa hai mặt phẳng (MCD), (EFCD) bằng
Câu 15:
Trong mặt phẳng (P) cho tam giác ABC có AB = 1, AC = 2, . Điểm S thay đổi thuộc đường thẳng đi qua A và vuông góc với (P), (S khác A). Gọi B1, C1 lần lượt là hình chiếu vuông góc của A trên SB, SC. Đường kính MN thay đổi của mặt cầu (T) ngoại tiếp khối đa diện ABCB1C1 và I là điểm cách tâm mặt cầu (T) một khoảng bằng ba lần bán kính. Tính giá trị nhỏ nhất của IM + IN.



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)