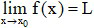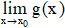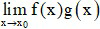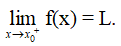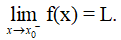160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án (P1)
160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án (P1) (Đề số 4)
-
1343 lượt thi
-
30 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 29:
07/11/2024Trong các giới hạn sau giới hạn nào bằng 0 ?
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Lời giải
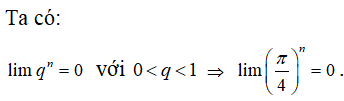
*Phương pháp giải:
Phương pháp giải:
- Rút lũy thừa có số mũ lớn nhất
- Áp dụng quy tắc giới hạn tới vô cực
|
|
|
|
|
L > 0 |
+∞ |
+∞ |
|
−∞ |
−∞ |
|
|
L < 0 |
+∞ |
−∞ |
|
−∞ |
+∞ |
*Lý thuyết :
Định nghĩa 1
Cho khoảng K chứa điểm x0 và hàm số y = f(x) xác định trên K hoặc trên K \ {x0}.
Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn ∈ K \{x0} và xn → x0, ta có f(xn) → L.
Kí hiệu: 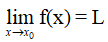
Nhận xét: 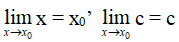
Định nghĩa 2
- Cho hàm số y = f(x) xác định trên (x0; b).
Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L.
Kí hiệu:
- Cho hàm số y = f(x) xác định trên (a; x0).
Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, a < xn < x0 và xn → x0, ta có f(xn) → L.
Kí hiệu:
Xem thêm
Lý thuyết Giới hạn của hàm số (mới + Bài Tập) – Toán 11
TOP 40 câu Trắc nghiệm Giới hạn của hàm số (có đáp án ) – Toán 11
Bài thi liên quan
-
160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án (P1) (Đề số 1)
-
30 câu hỏi
-
50 phút
-
-
160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án (P1) (Đề số 2)
-
30 câu hỏi
-
50 phút
-
-
160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án (P1) (Đề số 3)
-
30 câu hỏi
-
50 phút
-
-
160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án (P1) (Đề số 5)
-
33 câu hỏi
-
50 phút
-
Có thể bạn quan tâm
- 93 Bài tập trắc nghiệm Lượng giác lớp 11 có lời giải (P1) (1690 lượt thi)
- Bài tập Lượng giác ôn thi đại học có lời giải (P1) (386 lượt thi)
- 160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án (P1) (1342 lượt thi)
- Bài tập Giới hạn ôn thi đại học có lời giải (P1) (791 lượt thi)
- 15 câu lượng giác cơ bản , nâng cao (có đáp án) (p1) (358 lượt thi)
- Bài tập Lượng giác từ đề thi Đại học cơ bản, nâng cao (P1) (1066 lượt thi)
- 299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (3497 lượt thi)
- Bài tập Tổ Hợp - Xác Suất từ đề thi đại học cực hay có lời giải (P1) (1576 lượt thi)
- Bài tập Phép dời hình và phép đồng dạng trong mặt phẳng từ đề thi Đại Học (P1) (375 lượt thi)
- Bài tập Lượng giác từ đề thi đại học cơ bản, nâng cao có đáp án (P1) (1098 lượt thi)