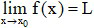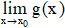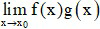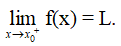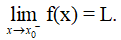Trong các giới hạn sau giới hạn nào bằng 0 ?

Đáp án đúng là C

Lời giải

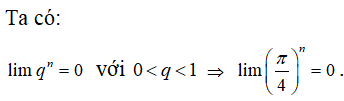
*Phương pháp giải:

Phương pháp giải:

- Rút lũy thừa có số mũ lớn nhất

- Áp dụng quy tắc giới hạn tới vô cực

L > 0	+∞	+∞
	−∞	−∞
L < 0	+∞	−∞
	−∞	+∞

*Lý thuyết :

Định nghĩa 1

Cho khoảng K chứa điểm x₀ và hàm số y = f(x) xác định trên K hoặc trên K \ {x₀}.

Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x₀ nếu với dãy số (x_n) bất kì, x_n ∈ K \{x₀} và x_n → x₀, ta có f(x_n) → L.

Kí hiệu: 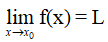 hay f(x) → L khi x → x₀.

Nhận xét: 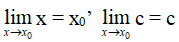 với c là hằng số.

Định nghĩa 2

- Cho hàm số y = f(x) xác định trên (x₀; b).

Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x₀ nếu với dãy số (x_n) bất kì, x₀ < x_n < b và x_n → x₀, ta có f(x_n) → L.

Kí hiệu: 

- Cho hàm số y = f(x) xác định trên (a; x₀).

Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x₀ nếu với dãy số (x_n) bất kì, a < x_n < x₀ và x_n → x₀, ta có f(x_n) → L.

Kí hiệu: 

Xem thêm

Lý thuyết Giới hạn của hàm số (mới  + Bài Tập) – Toán 11 

TOP 40 câu Trắc nghiệm Giới hạn của hàm số (có đáp án ) – Toán 11