Giải Vật lí 10 Bài 1 (Cánh diều): Chuyển động tròn

Giải bài tập Vật lí lớp 10 Bài 1: Chuyển động tròn

Mở đầu

Mở đầu trang 106 Vật lí 10:

Các đối tượng chuyển động tròn được gặp khá thường xuyên, ở mọi mức độ. Các bánh xe, bánh răng ròng rọc, vận động viên đua mô tô khi vào khúc quanh hay vệ tinh của Trái Đất – tất cả đều tham gia chuyển động tròn. Cái gì làm một vật chuyển động tròn? Sự hiểu biết về chuyển động tròn giữ vai trò quan trọng như thế nào trong cuộc sống, khoa học và kĩ thuật?

Lời giải:

Lực hướng tâm đã giữ cho vật chuyển động tròn.

Sự hiểu biết về chuyển động tròn giúp chúng ta chuyển động an toàn trên các đoạn đường cong, cua; giúp chúng ta xác định được lực cần thiết để giữ vật chuyển động tròn không bị văng ra khỏi quỹ đạo của chúng; giúp chúng ta tận dụng chuyển động li tâm để chế tạo máy giặt, máy vắt….

I. Mô tả chuyển động tròn

Câu hỏi 1 trang 106 Vật lí 10:

Lấy các ví dụ trong thực tế và thảo luận xem chuyển động nào là chuyển động tròn.

Lời giải:

- Chuyển động của các hành tinh quanh Mặt Trời là các chuyển động tròn.

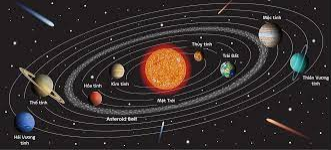
- Các xe chuyển động quanh vòng xuyến là chuyển động tròn.

- Chuyển động của đầu kim đồng hồ trên mặt số là chuyển động tròn.

1. Độ dịch chuyển góc và tốc độ góc

Luyện tập

Luyện tập 1 trang 107 Vật lí 10:

Đổi các góc sau từ độ sang radian: 30^o, 90^o, 105^o, 120^o, 270^o.

Lời giải:

Đổi các góc sau từ độ sang radian:

30^o = $\frac{\pi }{6}rad$,

90^o = $\frac{\pi }{2}$ rad,

105^o = $\frac{105}{360}.2\pi =\frac{7\pi }{12}$ rad.

120^o = $\frac{2\pi }{3}$ rad,

270^o = $\frac{3\pi }{2}$ rad.

Luyện tập 2 trang 107 Vật lí 10:

Đổi các góc sau từ radian sang độ: 0,5 rad; 0,75 rad; $\pi rad$.

Lời giải:

Đổi các góc sau từ radian sang độ:

0,5 rad = $\frac{0,5}{2\pi }{.360}^0=$ 28,64⁰ ;

0,75 rad = $\frac{0,75}{2\pi }{.360}^0=42,{97}^0$;

$\pi rad$ = 180⁰.

2. Tốc độ và vận tốc của chuyển động tròn đều.

Luyện tập 3, 4, 5 trang 108 Vật lí 10:

3. So sánh tốc độ chuyển động của đầu kim giây, đầu kim phút và đầu kim giờ?

4. Một đồng hồ chỉ 3h30ph. Hãy tính độ dịch chuyển góc từ vị trí 12h đến vị trí của kim phút và kim giờ.

5. Tính tốc độ góc của kim giờ và kim phút của đồng hồ.

Lời giải:

3. Kim giây chuyển động một vòng trong thời gian 1 phút, kim phút chuyển động một vòng trong thời gian 1 giờ, kim giờ chuyển động một vòng trong 12 giờ.

Vậy kim giây có tốc độ chuyển động nhanh nhất, kim phút có tốc độ chuyển động chậm hơn kim giây, kim giờ có tốc độ chuyển động chậm nhất.

4.

Vị trí 12h, cả kim giờ và kim phút đều chỉ số 12.

Khi đồng hồ chỉ 3 giờ 30 phút thì kim phút đã quay được một góc 180⁰, kim giờ quay được một góc là $\frac{3,5}{6}{.180}^0={105}^0$

5. Vì kim giờ quay một vòng trong thời gian 12 giờ nên tốc độ góc của kim giờ là:

${\omega }_1=\frac{2\pi }{\mathrm{12.60.60}}=\frac{\pi }{21600}(rad/s)$

Kim phút quay một vòng trong thời gian 1 giờ nên tốc độ góc của kim phút là:

${\omega }_2=\frac{2\pi }{60.60}=\frac{\pi }{1800}(rad/s)$

Câu hỏi 2 trang 108 Vật lí 10:

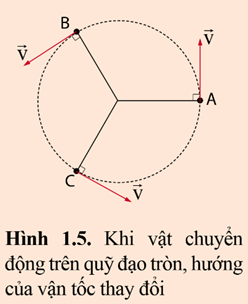
Giải thích vì sao toàn bộ các mũi tên trên hình 1.5 đều được vẽ với độ dài như nhau.

Lời giải:

Vì vật chuyển động tròn đều thì độ lớn vận tốc (tốc độ) không đổi, chỉ có hướng của vecto vận tốc thay đổi nên ta vẽ các vecto chỉ vận tốc dài như nhau.

3. Liên hệ giữa tốc độ và tốc độ góc

Luyện tập 6 trang 108 Vật lí 10:

Một em bé cưỡi ngựa gỗ trên sàn quay, ở cách trục quay 2,1 m. Tốc độ góc của sàn quay là 0,42 rad/s. Tính tốc độ của ngựa gỗ.

Lời giải:

Tốc độ của ngựa gỗ là v = ω.r = 0,42.2,1 = 0,882 (m/s)

Câu hỏi 3 trang 109 Vật lí 10:

Dựa vào đơn vị SI của các đại lượng, hãy chứng tỏ tính đúng đắn của biểu thức (4)

Lời giải:

Ta có biểu thức (4) $v=\omega r=\frac{2\pi }{T}.r$

Về thứ nguyên: [m/s] = [1/s].[m] = [m]/[s].

II. Lực hướng tâm và gia tốc hướng tâm

1. Lực hướng tâm

Câu hỏi 4 trang 109 Vật lí 10:

Lực gây ra gia tốc của chuyển động tròn đều có hướng như thế nào?

Lời giải:

Lực gây ra gia tốc của chuyển động tròn đều có phương dọc theo bán kính quỹ đạo và hướng vào tâm quỹ đạo tròn.

2. Gia tốc hướng tâm

Luyện tập 7 trang 110 Vật lí 10:

Hai điểm A và B nằm trên cùng một bán kính của một vô lăng đang quay đều, cách nhau 20 cm. Điểm A ở phía ngoài có tốc độ 0,6 m/s, điểm B ở phía trong (gần trục quay hơn) có tốc độ 0,2 m/s. Tính tốc độ góc của vô lăng.

Lời giải:

Gọi khoảng cách từ tâm đến điểm B là r (m) thì khoảng cách từ tâm đến điểm A là r + 0,2 (m).

Ta có: v_B = r.ω = 0,2 (m/s);

Và v_A = (r + 0,2).ω = 0,6 (m/s) $\iff$ r.ω + 0,2ω = 0,6 $\iff$ ω = 0,4:0,2 = 2 (rad/s)

Vậy tốc độ góc của vô lăng là 2 rad/s.

Luyện tập 8 trang 110 Vật lí 10:

Áp dụng định luật II Newton hãy rút ra biểu thức tính độ lớn của lực hướng tâm.

Lời giải:

Ta có $F=m.a_{ht}=m.\frac{{\nu }^2}{r}=m.r.{\omega }^2$

Vận dụng 1 trang 110 Vật lí 10:

Trạm không gian quốc tế ISS có tổng khối lượng 350 tấn, quay quanh Trái Đất ở độ cao 340 km, nơi có gia tốc trọng trường 8,8 m/s². Bán kính Trái Đất là 6400 km. Tính:

a) Lực hướng tâm tác dụng lên Trạm không gian.

b) Tốc độ của Trạm không gian trên quỹ đạo.

c) Thời gian Trạm không gian quay một vòng quanh Trái Đất.

d) Số vòng Trạm không gian quay quanh Trái Đất trong một ngày.

Lời giải:

Đổi đơn vị: m = 350 tấn = 350000 kg; h = 240 km = 240000 m; R = 6400 km = 6400000 m

a) Lực hấp dẫn do Trái Đất tác dụng lên trạm vũ trụ đóng vai trò lực hướng tâm

F = ma = 350000.8,8 = 3080000 (N)

b) Lực hấp dẫn đóng vai trò lực hướng tâm nên

$F=m\frac{v^2}{r}\Rightarrow v=\sqrt{\frac{F.r}{m}}=\sqrt{\frac{3080000.(6400000+240000)}{350000}}=7644\left(m/s\right)$

c) Thời gian quay quanh Trái Đất của Trạm không gian là:

$T=\frac{2\pi r}{v}=\frac{2\pi (6400000+240000)}{7644}=5457,8$ (s) = 1,517 giờ

d) Số vòng Trạm không gian thực hiện quanh Trái Đất trong một ngày là

$N=\frac{24}{T}=\frac{24}{1,516}=15,83$ (vòng).

3. Lực hướng tâm và một số tình huống chuyển động tròn trong thực tế

Câu hỏi 5 trang 110 Vật lí 10:

Trong hình 1.8, ô tô muốn rẽ với đoạn đường cong rộng hơn và với tốc độ lớn hơn. Làm thế nào để người lái xe rẽ trái an toàn?

Lời giải:

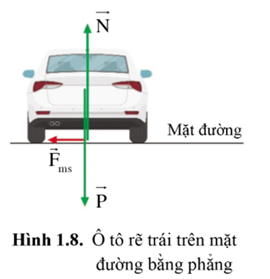
Lực ma sát đóng vai trò lực hướng tâm phải thỏa mãn điều kiện $F=\frac{m{v}^2}{r}$ để ô tô rẽ trái an toàn với tốc độ v và bán kính quỹ đạo r mong muốn.

Nếu lực ma sát không đủ lớn thì xe sẽ không đi qua được khúc cua như ý muốn của người lái xe.

Để ô tô rẽ trái an toàn hơn thì mặt đường ở chỗ cua làm nghiêng đi một chút về phía trái, như vậy có thêm hợp của hai lực P và N tác dụng lên xe đóng vai trò lực hướng tâm, giúp xe ôm cua an toàn hơn (như hình vẽ).

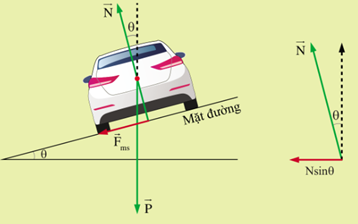
Tìm hiểu thêm trang 111 Vật lí 10:

Khi chiếc ô tô chuyển động trên mặt đường nghiêng với góc nghiêng nhỏ (hình 1.9), thì các thành phần theo phương thẳng đứng của phản lực N và của lực ma sát cân bằng với trọng lực P = mg của xe, còn các thành phần theo phương nằm ngang của phản lực N và của lực ma sát đóng vai trò lực hướng tâm. Do đó, theo phương ngang

$N\sin \theta +F_{ms}\cos \theta =\frac{m{v}^2}{r}$

Với r là bán kính của cung đường, v là tốc độ của xe.

Thảo luận về các yếu tố ảnh hưởng của góc nghiêng của mặt đường tới sự an toàn của xe khi vào khúc đường quanh tròn.

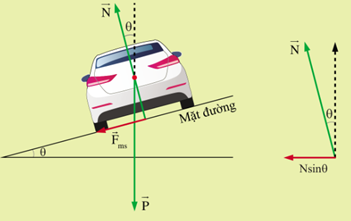
Lời giải:

Nếu góc nghiêng của mặt đường lớn mà tốc độ của ô tô không đủ lớn để thỏa mãn biểu thức $N\sin \theta +F_{ms}\cos \theta =\frac{m{v}^2}{r}$ thì xe sẽ bị trượt trên đường. Nếu lực ma sát không đủ lớn để giữ ô tô thì xe sẽ bị trôi ra khỏi mặt đường, gây mất an toàn.

Ngược lại, nếu chuyển động với tốc độ lớn thì có nguy cơ mất tay lái hoặc không xử lí kịp khi gặp vật cản cũng gây ra nguy hiểm cho người ngồi trên xe.

Vận dụng 2 trang 112 Vật lí 10:

Trong mỗi tình huống trong hình 1.10, lực nào đóng vai trò là lực hướng tâm? Thảo luận về các điều kiện đảm bảo an toàn của chuyển động trong mỗi tình huống.

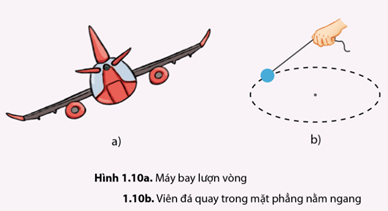
1. Chiếc máy bay đang lượn vòng. Để chuyển hướng, người phi công làm nghiêng cánh máy bay (hình 1.10a).

2. Một viên đá được buộc vào một sợi dây và quay tròn trong mặt phẳng ngang tạo thành hình nón (hình 1.10b).

Lời giải:

1. Chiếc máy bay đang lượn vòng. Để chuyển hướng, người phi công làm nghiêng cánh máy bay, khi đó hợp lực của trọng lực và lực nâng của không khí tác dụng lên máy bay đóng vai trò lực hướng tâm.

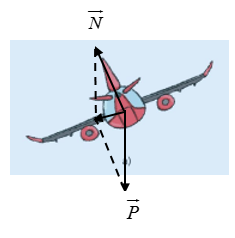
Khi nghiêng máy bay cần chú ý góc nghiêng và vận tốc chuyển động của máy báy, nếu góc nghiêng lớn, hợp lực lớn, còn vận tốc chuyển động của máy bay không đủ thì lực này làm cho máy bay bị đẩy ra khỏi quỹ đạo chuyển động, mất thăng bằng, có thể bị lật. Ngược lại, chuyển động với vận tốc lớn mà góc nghiêng không đủ thì máy bay không chuyển hướng theo ý muốn của phi công được, có thể bị mất lái và nguy hiểm.

2. Một viên đá được buộc vào một sợi dây và quay tròn trong mặt phẳng ngang tạo thành hình nón, hợp lực của trọng lực và lực căng dây đóng vai trò lực hướng tâm.

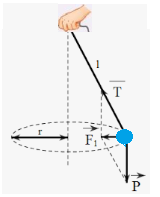
Nếu vật chuyển động với vận tốc càng lớn thì bán kính quỹ đạo r càng tăng và lực căng dây cũng càng lớn, khi đó góc lệch giữa sợi dây và phương thẳng đứng cũng tăng.

Nếu vật chuyển động với vận tốc quá lớn và lực căng dây vượt quá giới hạn đàn hồi của dây thì dây có thể bị đứt hoặc vật bị tuột và văng ra theo phương tiếp tuyến với quỹ đạo tròn.

Lý thuyết Chuyển động tròn

I. Mô tả chuyển động tròn.

- Một vật chuyển động tròn khi nó di chuyển trên một đường tròn.

- Ví dụ: Đầu kim đồng hồ chuyển động trên mặt số là chuyển động tròn.

1. Độ dịch chuyển góc và tốc độ góc

- Giả sử một vật chuyển động trên một đường tròn bán kính r. Trong thời gian t vật đi được quãng đường s. Góc $\theta$ ứng với cung tròn s mà vật đã đi được kể từ vị trí ban đầu gọi là độ dịch chuyển góc. Độ dịch chuyển góc $\theta$ được xác định bởi:

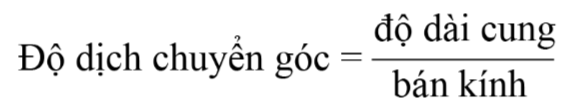
hay $\theta =\frac{s}{r}$

- Đơn vị của độ dịch chuyển góc là radian, kí hiệu là rad. Nếu s = r thì $\theta =1rad$

- 1 radian là một góc ở tâm ứng với một cung có độ dài bằng bán kính của đường tròn.

- Đại lượng được xác định bởi độ dịch chuyển góc trong một đơn vị thời gian gọi là tốc độ góc:

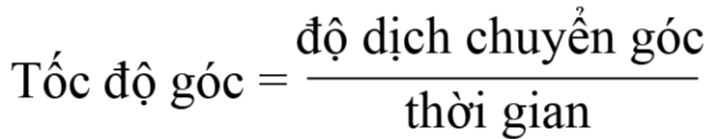
hay $\omega =\frac{\theta }{t}$

- Trong đó $\omega$ là tốc độ góc. Đơn vị của tốc độ góc là radian trên giây (rad/s)

2. Tốc độ và vận tốc của chuyển động tròn đều

- Một vật chuyển động tròn đều khi nó di chuyển trên một đường tròn với tốc độ không đổi, tức là vật dịch chuyển được các cung tròn có số đo góc như nhau sau những khoảng thời gian bằng nhau.

- Tốc độ của chuyển động tròn đều là không đổi nên tốc độ này bằng độ dài đường tròn chia cho thời gian đi hết một vòng:

$v=\frac{2\pi r}{T}$

Trong đó: r là bán kính của đường tròn.

T là chu kì (thời gian vật đi hết một vòng)

- Vận tốc của chuyển động tròn tại mỗi điểm trên quỹ đạo có phương tiếp tuyến với quỹ đạo tại điểm đó.

3. Liên hệ giữa tốc độ và tốc độ góc.

- Tốc độ v của chuyển động tròn phụ thuộc vào hai đại lượng: tốc độ góc $\omega$ và khoảng cách r từ vật đến tâm quỹ đạo:

Tốc độ = tốc độ góc $\times$ bán kính

hay: $v=\omega .r$

II. Lực hướng tâm và gia tốc hướng tâm.

1. Lực hướng tâm

- Vận tốc của chuyển động tròn đều luôn luôn thay đổi vì hướng liên tục thay đổi, cho dù độ lớn của nó không đổi. Và bởi vì vận tốc liên tục thay đổi, nên chuyển động tròn đều là chuyển động có gia tốc.

- Lực tác dụng lên vật luôn hướng vào tâm quỹ đạo tròn nên được gọi là lực hướng tâm.

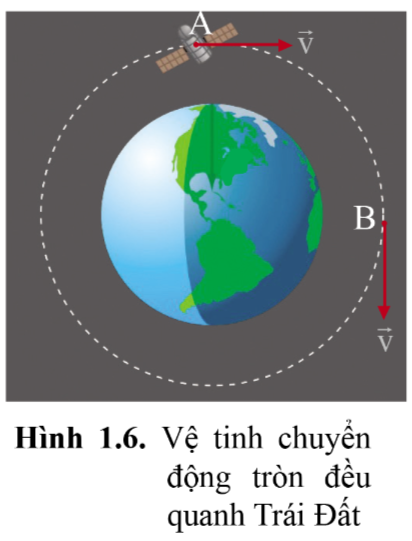
Lực hấp dẫn đóng vai trò lực hướng tâm

2. Gia tốc hướng tâm

- Vật chuyển động tròn đều chịu tác dụng của lực hướng tâm. Theo định luật II Newton lực hướng tâm gây ra gia tốc cho vật, gia tốc này có cùng hướng với hướng của lực hướng tâm, nghĩa là luôn hướng vào tâm của quỹ đạo tròn nên được gọi là gia tốc hướng tâm.

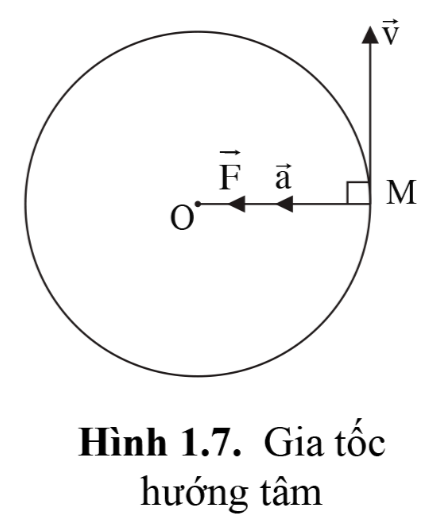
- Gia tốc hướng tâm có liên hệ với tốc độ v và bán kính quỹ đạo r theo biểu thức:

$a=\frac{v^2}{r}$ hoặc $a=r.{\omega }^2$

3. Lực hướng tâm và một số tình huống chuyển động tròn trong thực tế.

- Một vài tình huống chuyển động tròn trong thực tế, trong đó lực hướng tâm không thấy rõ ràng ngay từ đầu và liên quan mật thiết đến mức độ an toàn của chuyển động:

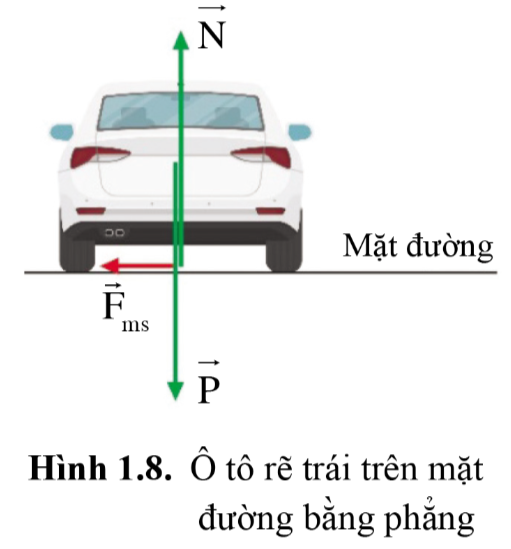
Lực ma sát đóng vai trò lực hướng tâm

Xem thêm lời giải bài tập Vật lí lớp 10 Cánh diều hay, chi tiết khác:

Bài 1: Động lượng và định luật bảo toàn động lượng

Bài 2: Động lượng và năng lượng trong va chạm

Bài tập chủ đề 4

Bài 2: Sự biến dạng

Bài tập chủ đề 5

Xem thêm tài liệu Vật lí lớp 10 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Chuyển động tròn

Trắc nghiệm Bài 1: Chuyển động tròn