Cho 0 < anpha < pi/2. Xác định dấu của các giá trị lượng giác
Với giải Bài 3 trang 148 sgk Toán lớp 10 Đại số được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải Toán 10 Bài 2: Giá trị lượng giác của một cung
Video Giải Bài 3 trang 148 Toán lớp 10 Đại số
Bài 3 trang 148 Toán lớp 10 Đại số: Cho 0<α<π20<α<π2. Xác định dấu của các giá trị lượng giác
a) sin(α−π)sin(α−π);
b) cos(3π2−α)cos(3π2−α);
c) tan(α+π)tan(α+π);
d) cot(α+π2)cot(α+π2).
*Lời giải:
a) Với 0<α<π20<α<π2, ta có:
sinα>0,cosα>0,tanα>0,cotα>0sinα>0,cosα>0,tanα>0,cotα>0
sin(α−π)sin(α−π)
=sin[−(π−α)]=sin[−(π−α)]
=−sin(π−α)=−sin(π−α) (áp dụng sin(–x) = –sinx với x=π−αx=π−α)
= −sinα−sinα (áp dụng sin(π−x)=sinxsin(π−x)=sinx với x=αx=α)
Mà sinα>0sinα>0 khi 0<α<π20<α<π2 nên −sinα<0−sinα<0 hay sin(α−π)<0sin(α−π)<0
b) Ta có: cos(3π2−α)cos(3π2−α)
=cos(π+π2−α)=cos(π+π2−α)
=−cos(π2−α)=−cos(π2−α)
(áp dụng cos(π+x)=−cosxcos(π+x)=−cosx với x=π2−αx=π2−α)
=−sinα=−sinα (áp dụng cos(π2−x)=sinxcos(π2−x)=sinx với x=αx=α)
Mà sinα>0sinα>0 khi 0<α<π20<α<π2 nên −sinα<0−sinα<0 hay cos(3π2−α)<0cos(3π2−α)<0
c) Ta có: tan(α+π)=tanαtan(α+π)=tanα
Mà tanα>0tanα>0 khi 0<α<π20<α<π2 nên tan(α+π)>0tan(α+π)>0
d) Ta có:
cot(π2+α)=cot[π2−(−α)]=tan(−α)=−tanα
Mà khi 0<α<π2 nên −tanα<0 hay cot(π2+α)<0
*Phương pháp giải
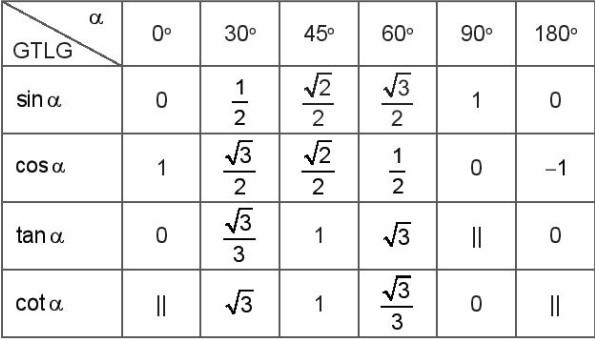
*Một số lý thuyết và dạng bài tập về giá trị lượng giác của một cung:
1. Đồ thị và tính chất của hàm số y = sinx
- Tập xác định là R.
- Tập giá trị là [-1;1].
- Là hàm số lẻ và tuần hoàn chu kì 2π.
- Đồng biến trên mỗi khoảng (−π2+k2π;π2+k2π) và nghịch biến trên mỗi khoảng (π2+k2π;3π2+k2π)
- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.
2. Đồ thị và tính chất của hàm số y = cosx
Tập xác định là R.
Tập giá trị là [-1;1].
Là hàm số chẵn và tuần hoàn chu kì 2π.
Đồng biến trên mỗi khoảng (−π+k2π;k2π) và nghịch biến trên mỗi khoảng (k2π;π+k2π).
Có đồ thị là một đường hình sin đối xứng qua trục tung.
Hệ quả:
+) sinα, cosα xác định với mọi giá trị của α và −1≤sinα≤1, −1≤cosα≤1.
+) tanα được xác định khi α≠π2+kπ, xác định khi α≠kπ
+) sinα=sin(α+k2π), cosα=cos(α+k2π)
tanα=tan(α+kπ), cotα=cot(α+kπ)
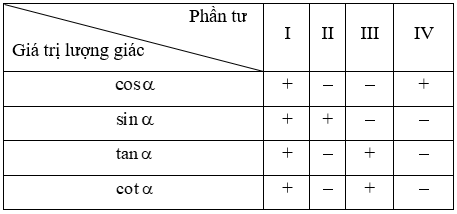
+) Dấu của các giá trị lượng giác phụ thuộc vào vị trí điểm M nằm trên đường tròn lượng giác.
Ta có bảng xác định dấu của các giá trị lượng giác:
Các công thức lượng giác cơ bản:

Các dạng bài
Dạng 1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị
a. Phương pháp giải:
Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.
Dạng 2: Chứng minh một đẳng thức giữa các giá trị lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.
Ta lựa chọn một trong các cách biến đổi sau:
* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)
* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.
Dạng 3: Rút gọn biểu thức lượng giác
a. Phương pháp giải:
Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.
Xem thêm các bài viết liên quan hay, chi tiết
Toán 10 Bài 2 giải vở bài tập: Giá trị lượng giác của một cung
Trắc nghiệm Giá trị lượng giác của một cung (có đáp án)
Xem thêm lời giải bài tập Toán lớp 10 hay, chi tiết khác:
Hoạt động 1 trang 141 Toán 10 Đại số: Nhắc lại khái niệm giá trị lượng giác...
Hoạt động 2 trang 142 Toán 10 Đại số: Tính...
Hoạt động 3 trang 143 Toán 10 Đại số: Từ định nghĩa và ...
Hoạt động 4 trang 145 Toán 10 Đại số: Từ ý nghĩa hình học của và ...
Hoạt động 5 trang 145 Toán 10 Đại số: Từ định nghĩa của và ...
Hoạt động 6 trang 148 Toán 10 Đại số: Tính cos(−11π4)...
Bài 1 trang 148 Toán 10 Đại số: Có cung nào mà nhận...
Bài 2 trang 148 Toán 10 Đại số: Các đẳng thức sau có thể đồng...
Bài 4 trang 148 Toán 10 Đại số: Tính các giá trị lượng giác của góc ...
Xem thêm các chương trình khác:
- Soạn văn 10 (hay nhất) | Để học tốt Ngữ Văn 10 (sách mới)
- Soạn văn 10 (ngắn nhất) | Để học tốt Ngữ văn 10 (sách mới)
- Văn mẫu lớp 10 (cả ba sách) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Lịch sử 10 | Giải bài tập Lịch sử 10 Học kì 1, Học kì 2 (sách mới)
- Đề thi Lịch sử 10
- Bài tập Tiếng Anh 10 theo Unit (sách mới) có đáp án
- Giải sgk Tiếng Anh 10 (thí điểm)
