Câu hỏi:
06/11/2024 254
Trong không gian Oxyz, phương trình của mặt phẳng (Oxy) là:
Trong không gian Oxyz, phương trình của mặt phẳng (Oxy) là:
A. z = 0.
A. z = 0.
B. x = 0.
B. x = 0.
C. y = 0.
D. x + y = 0.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A
*Lời giải:
Phương trình mặt phẳng (Oxy) là z = 0.
*Phương pháp giải:
Mặt phẳng (Oxy) là tập hợp các điểm có cao độ z = 0 nên có phương trình: z = 0.
*Cách giải và các dạng bài toán về hệ trục tọa độ trong không gian:
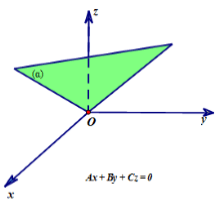
Phương trình tổng quát của mặt phẳng
- Trong không gian Oxy , mọi mặt phẳng đều có dạng phương trình:
Ax + By + Cz + D = 0 với A2 + B2 + C2 ≠ 0
- Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì nó có một VTPT là n→(A; B; C).
- Phương trình mặt phẳng đi qua điểm Mo(xo; yo; zo) và nhận vectơ n→(A; B; C) khác 0→ là VTPT là: A(x - xo) + B(y - yo) + C(z - zo) = 0 .
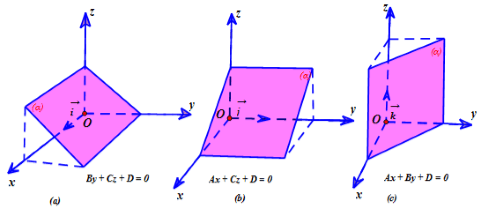
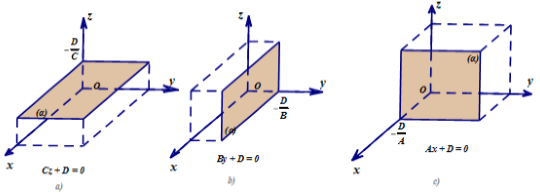
• Các trường hợp riêng
Xét phương trình mặt phẳng (α): Ax + By + Cz + D = 0 với A2 + B2 + C2 ≠ 0
- Nếu D = 0 thì mặt phẳng (α) đi qua gốc tọa độ O.
- Nếu A = 0, B ≠ 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Ox.
- Nếu A ≠ 0, B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Oy.
- Nếu A ≠ 0, B ≠ 0, C = 0 thì mặt phẳng (α) song song hoặc chứa trục Oz.
- Nếu A = B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxy).
- Nếu A = C = 0, B ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxz).
- Nếu B = C = 0, A ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oyz).
Chú ý:
- Nếu trong phương trình (α) không chứa ẩn nào thì (α) song song hoặc chứa trục tương ứng.
- Phương trình mặt phẳng theo đoạn chắn (α): 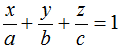
Khoảng cách từ một điểm đến một mặt phẳng.
• Trong không gian Oxyz, cho điểm Mo(xo; yo; zo) và mặt phẳng (α): Ax + By + Cz + D = 0
Khi đó khoảng cách từ điểm Mo đến mặt phẳng (α) được tính:
Góc giữa hai mặt phẳng
Trong không gian Oxyz, cho hai mặt phẳng (α): A1x + B1y + C1z + D1 = 0 và (β): A2x + B2y + C2z + D2 = 0
Góc giữa (α) và (β) bằng hoặc bù với góc giữa hai VTPT nα→, nβ→. Tức là:
Một số dạng bài tập về viết phương trình mặt phẳng
Dạng 1: Viết phương trình mặt phẳng khi biết một điểm và vectơ pháp tuyến của nó.
Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.
Dạng 2: Viết phương trình mặt phẳng (α) đi qua 1 điểm Mo(xo; yo; zo) và song song với 1 mặt phẳng (β): Ax + By + Cz + D = 0 cho trước.
Cách 1: Thực hiện theo các bước sau:
1. VTPT của (β) là nβ→ = (A; B; C)
2. (α) // (β) nên VTPT của mặt phẳng (α) là nα→ = nβ→ = (A; B; C)
3. Phương trình mặt phẳng (α): A(x - x0) + B(y - y0) + C(z - z0) = 0
Cách 2:
1. Mặt phẳng (α) // (β) nên phương trình (P) có dạng: Ax + By + Cz + D' = 0 (*), với D' ≠ D.
2. Vì (P) qua 1 điểm Mo(xo; yo; zo) nên thay tọa độ Mo(xo; yo; zo) vào (*) tìm được D'.
Dạng 3: Viết phương trình mặt phẳng (α) đi qua 3 điểm A, B, C không thẳng hàng.
1. Tìm tọa độ các vectơ: AB→, AC→
2. Vectơ pháp tuyến của (α) là: nα→ = [AB→, AC→]
3. Điểm thuộc mặt phẳng: A (hoặc B hoặc C).
4. Viết phương trình mặt phẳng qua 1 điểm và có VTPT nα
Dạng 4: Viết phương trình mặt phẳng (α) đi qua điểm M và vuông góc với đường thẳng Δ
1. Tìm VTCP của Δ là uΔ→
2. Vì (α) ⊥ Δ nên (α) có VTPT nα→ = uΔ→
3. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT nα→
Dạng 5: Viết phương trình mặt phẳng (α) chứa đường thẳng Δ, vuông góc với mặt phẳng (β)
1. Tìm VTPT của (β) là nβ→
2. Tìm VTCP của Δ là uΔ→
3. VTPT của mặt phẳng (α) là: nα→ = [nβ→; uΔ→]
4. Lấy một điểm M trên Δ
5. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.
Dạng 6: Viết phương trình mặt phẳng (α) qua hai điểm A, B và vuông góc với mặt phẳng (β)
1. Tìm VTPT của (β) là nβ→
2. Tìm tọa độ vectơ AB→
3. VTPT của mặt phẳng (α) là: nα→ = [nβ→, AB→]
4. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Hệ trục toạ độ trong không gian– Toán lớp 12 Kết nối tri thức
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên

Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g'(x) thuộc khoảng nào dưới đây?
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên

Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g'(x) thuộc khoảng nào dưới đây?
Câu 2:
Biết F(x); G(x) là hai nguyên hàm của hàm số f(x) trên và = F(4) − G(0) + a (a > 0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F(x); y = G(x); x = 0; x = 4. Khi S = 8 thì a bằng
Biết F(x); G(x) là hai nguyên hàm của hàm số f(x) trên và = F(4) − G(0) + a (a > 0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F(x); y = G(x); x = 0; x = 4. Khi S = 8 thì a bằng
Câu 3:
Cho hàm số f(x) = ax4 + 2(a + 4)x2 − 1 với a là tham số thực. Nếu = f(1) thì bằng
Cho hàm số f(x) = ax4 + 2(a + 4)x2 − 1 với a là tham số thực. Nếu = f(1) thì bằng
Câu 5:
Lời giải:
Với a,b là các số thực dương tùy ý và a ≠ 1, bằng
*Phương pháp giải:
a. Đưa về cùng cơ số
- Áp dụng một số tính chất của lôgarit:
b. Đặt ẩn phụ
c. Mũ hóa.
*LÝ thuyết :
- Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
- Phương trình lôgarit cơ bản có dạng:
Theo định nghĩa lôgarit ta có:
Xem thêm
Phương trình lôgarit | Lý thuyết, công thức, các dạng bài tập và cách giải
Lời giải:
Với a,b là các số thực dương tùy ý và a ≠ 1, bằng
*Phương pháp giải:
a. Đưa về cùng cơ số
- Áp dụng một số tính chất của lôgarit:
b. Đặt ẩn phụ
c. Mũ hóa.
*LÝ thuyết :
- Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
- Phương trình lôgarit cơ bản có dạng:
Theo định nghĩa lôgarit ta có:
Xem thêm
Phương trình lôgarit | Lý thuyết, công thức, các dạng bài tập và cách giải
Câu 6:
Cho khối nón có diện tích đáy bằng 3a2 và chiều cao 2a. Thể tích của khối nón đã cho bằng ?
Cho khối nón có diện tích đáy bằng 3a2 và chiều cao 2a. Thể tích của khối nón đã cho bằng ?
Câu 7:
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (4b − 1)(a.3b − 10) < 0 ?
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (4b − 1)(a.3b − 10) < 0 ?
Câu 8:
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 3. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của S bằng
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 3. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của S bằng
Câu 9:
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong hình bên.
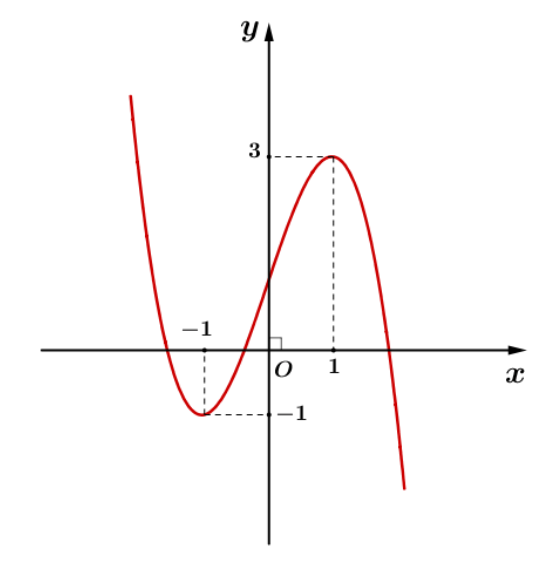
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong hình bên.

Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ
Câu 10:
Có bao nhiêu giá trị nguyên âm của tham số a để hàm số y = |x4 + ax2 – 8x| có đúng 3 điểm cực trị?
Có bao nhiêu giá trị nguyên âm của tham số a để hàm số y = |x4 + ax2 – 8x| có đúng 3 điểm cực trị?
Câu 11:
Trong không gian Oxyz, cho điểm M (2; −2;1) và mặt phẳng (P) : 2x − 3y − z + 1 = 0. Đường thẳng đi qua M và vuông góc với (P) có phương trình là
Trong không gian Oxyz, cho điểm M (2; −2;1) và mặt phẳng (P) : 2x − 3y − z + 1 = 0. Đường thẳng đi qua M và vuông góc với (P) có phương trình là
Câu 12:
Cho các số phức z1, z2, z3 thỏa mãn 2 = 2 = = 2 và (z1 + z2)z3 = 3z1z2 . Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
Cho các số phức z1, z2, z3 thỏa mãn 2 = 2 = = 2 và (z1 + z2)z3 = 3z1z2 . Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng

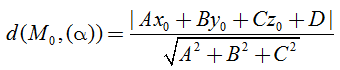
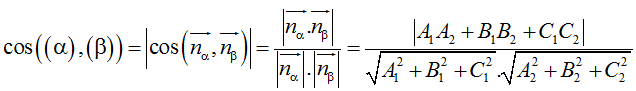


![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)