Câu hỏi:
19/07/2024 282
Trong không gian Oxyz, cho mặt cầu (S) tâm I(9; 3; 1) bán kính bằng 3 . Gọi M, N là hai điểm lần lượt thuộc 2 trục Ox, Oz sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và (s), giá trị AM. AN bằng
Trong không gian Oxyz, cho mặt cầu (S) tâm I(9; 3; 1) bán kính bằng 3 . Gọi M, N là hai điểm lần lượt thuộc 2 trục Ox, Oz sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng . Gọi A là tiếp điểm của MN và (s), giá trị AM. AN bằng
A. 12 .
A. 12 .
B. 18.
B. 18.
C. 28 .
D. 39.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
I(9; 3 ; 1) d = 3 = R Þ (S) tiếp xúc với (Oxz)
Gọi M( a; 0; 0) Î Ox
N(0; 0; b) Î Oz
MN tiếp xúc với (S) tại A nên A là hình chiếu của I lên (Oxz)
Suy ra A(9; 0; 1)
Gọi K là trung điểm MN Þ K
Gọi H là tâm mặt cầu ngoại tiếp tứ diện OIMN Þ OH = Þ HK MN
Gọi T là trung điểm OM Þ Þ OM (KHT)
Þ OM HK Þ HK (OMN)
Mà IA (OMN) Þ HK// IA
Ta có : = (0; 3; 0)
=
cùng phương nên
H
ỌH = + c2 + = (1)
HI = OH = + + = (2)
Từ (1) và (2) suy ra + c2 + = + +
9a + b + 6c = 91 (3)
= (a − 9; 0; −1)
= (−9; 0; b − 1)
A, M, N thẳng hàng
(a − 2)(b − 1) = 9
ab − a − 9b + 9 = 9
ab − a − 9b = 0
a(b − 1) = 9b
a =
Từ (3) 9. + b + 6c = 91
+ b + 6c = 91
+ 6c = 91 6c = 91 − =
c =
Ta có a2 + 4c2 + b2 = 169
+ 4 + b2 = 169
9.81b2 + (b4 + 121b2 +8281− 22b3 + 182b2 − 2002b) + 9b2(b − 1)2 = 169 . 9 . (b − 1)2
729b2 + b4 +121b2 +8281 − 22b3 + 182b2 − 2002b + 9b4 − 18b3 +9b2 = 1521b2 − 3042b +1521
10b4 − 40b3 − 480b2 + 1040b +6760 = 0
+ Trường hợp 1: a = 9 + ; b = 1 + 3 Þ = Þ AM = 2
Þ = ÞAN =
AM.AN = 2. = 12
+ Trường hợp 2: a = 9 − ; b = 1 − 3 Þ = Þ AM = 2
Þ = Þ AN =
AM.AN = 2. = 12
Đáp án đúng là: A
I(9; 3 ; 1) d = 3 = R Þ (S) tiếp xúc với (Oxz)
Gọi M( a; 0; 0) Î Ox
N(0; 0; b) Î Oz
MN tiếp xúc với (S) tại A nên A là hình chiếu của I lên (Oxz)
Suy ra A(9; 0; 1)
Gọi K là trung điểm MN Þ K
Gọi H là tâm mặt cầu ngoại tiếp tứ diện OIMN Þ OH = Þ HK MN
Gọi T là trung điểm OM Þ Þ OM (KHT)
Þ OM HK Þ HK (OMN)
Mà IA (OMN) Þ HK// IA
Ta có : = (0; 3; 0)
=
cùng phương nên
H
ỌH = + c2 + = (1)
HI = OH = + + = (2)
Từ (1) và (2) suy ra + c2 + = + +
9a + b + 6c = 91 (3)
= (a − 9; 0; −1)
= (−9; 0; b − 1)
A, M, N thẳng hàng
(a − 2)(b − 1) = 9
ab − a − 9b + 9 = 9
ab − a − 9b = 0
a(b − 1) = 9b
a =
Từ (3) 9. + b + 6c = 91
+ b + 6c = 91
+ 6c = 91 6c = 91 − =
c =
Ta có a2 + 4c2 + b2 = 169
+ 4 + b2 = 169
9.81b2 + (b4 + 121b2 +8281− 22b3 + 182b2 − 2002b) + 9b2(b − 1)2 = 169 . 9 . (b − 1)2
729b2 + b4 +121b2 +8281 − 22b3 + 182b2 − 2002b + 9b4 − 18b3 +9b2 = 1521b2 − 3042b +1521
10b4 − 40b3 − 480b2 + 1040b +6760 = 0
+ Trường hợp 1: a = 9 + ; b = 1 + 3 Þ = Þ AM = 2
Þ = ÞAN =
AM.AN = 2. = 12
+ Trường hợp 2: a = 9 − ; b = 1 − 3 Þ = Þ AM = 2
Þ = Þ AN =
AM.AN = 2. = 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên

Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g'(x) thuộc khoảng nào dưới đây?
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên

Diện tích hình phẳng giới hạn bởi các đường y = f '(x) và y = g'(x) thuộc khoảng nào dưới đây?
Câu 2:
Biết F(x); G(x) là hai nguyên hàm của hàm số f(x) trên và = F(4) − G(0) + a (a > 0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F(x); y = G(x); x = 0; x = 4. Khi S = 8 thì a bằng
Biết F(x); G(x) là hai nguyên hàm của hàm số f(x) trên và = F(4) − G(0) + a (a > 0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F(x); y = G(x); x = 0; x = 4. Khi S = 8 thì a bằng
Câu 3:
Cho hàm số f(x) = ax4 + 2(a + 4)x2 − 1 với a là tham số thực. Nếu = f(1) thì bằng
Cho hàm số f(x) = ax4 + 2(a + 4)x2 − 1 với a là tham số thực. Nếu = f(1) thì bằng
Câu 5:
Lời giải:
Với a,b là các số thực dương tùy ý và a ≠ 1, bằng
*Phương pháp giải:
a. Đưa về cùng cơ số
- Áp dụng một số tính chất của lôgarit:
b. Đặt ẩn phụ
c. Mũ hóa.
*LÝ thuyết :
- Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
- Phương trình lôgarit cơ bản có dạng:
Theo định nghĩa lôgarit ta có:
Xem thêm
Phương trình lôgarit | Lý thuyết, công thức, các dạng bài tập và cách giải
Lời giải:
Với a,b là các số thực dương tùy ý và a ≠ 1, bằng
*Phương pháp giải:
a. Đưa về cùng cơ số
- Áp dụng một số tính chất của lôgarit:
b. Đặt ẩn phụ
c. Mũ hóa.
*LÝ thuyết :
- Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
- Phương trình lôgarit cơ bản có dạng:
Theo định nghĩa lôgarit ta có:
Xem thêm
Phương trình lôgarit | Lý thuyết, công thức, các dạng bài tập và cách giải
Câu 6:
Cho khối nón có diện tích đáy bằng 3a2 và chiều cao 2a. Thể tích của khối nón đã cho bằng ?
Cho khối nón có diện tích đáy bằng 3a2 và chiều cao 2a. Thể tích của khối nón đã cho bằng ?
Câu 7:
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (4b − 1)(a.3b − 10) < 0 ?
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (4b − 1)(a.3b − 10) < 0 ?
Câu 8:
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 3. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của S bằng
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 3. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của S bằng
Câu 9:
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong hình bên.
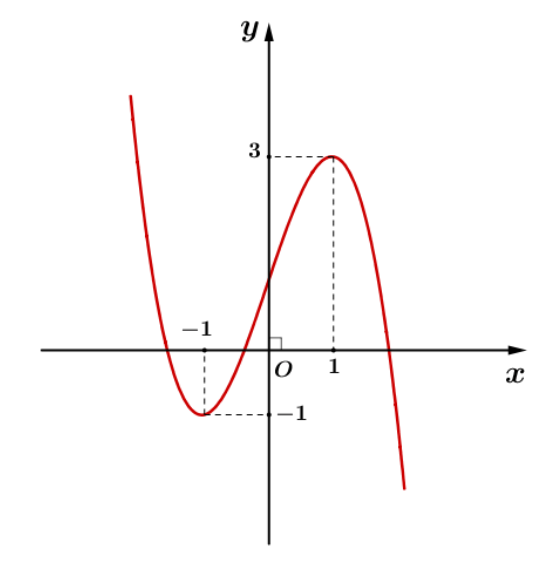
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong hình bên.

Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ
Câu 10:
Có bao nhiêu giá trị nguyên âm của tham số a để hàm số y = |x4 + ax2 – 8x| có đúng 3 điểm cực trị?
Có bao nhiêu giá trị nguyên âm của tham số a để hàm số y = |x4 + ax2 – 8x| có đúng 3 điểm cực trị?
Câu 11:
Trong không gian Oxyz, cho điểm M (2; −2;1) và mặt phẳng (P) : 2x − 3y − z + 1 = 0. Đường thẳng đi qua M và vuông góc với (P) có phương trình là
Trong không gian Oxyz, cho điểm M (2; −2;1) và mặt phẳng (P) : 2x − 3y − z + 1 = 0. Đường thẳng đi qua M và vuông góc với (P) có phương trình là
Câu 12:
Cho các số phức z1, z2, z3 thỏa mãn 2 = 2 = = 2 và (z1 + z2)z3 = 3z1z2 . Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng
Cho các số phức z1, z2, z3 thỏa mãn 2 = 2 = = 2 và (z1 + z2)z3 = 3z1z2 . Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)