Câu hỏi:
06/11/2024 290
Trong không gian Oxyz, cho ba điểm Gọi (P) là mặt phẳng chứa BC và cách A một khoảng lớn nhất. Hỏi vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng (P)?
Trong không gian Oxyz, cho ba điểm Gọi (P) là mặt phẳng chứa BC và cách A một khoảng lớn nhất. Hỏi vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng (P)?
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: D
*Lời giải:
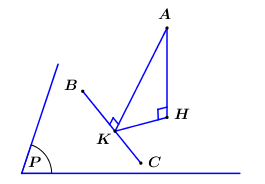
Gọi H, K lần lượt là hình chiếu vuông góc của A lên (P), BC.
Ta có vuông tại hay .
Do đó d(A; (P)) lớn nhất khi
Ta có Phương trình đường thẳng
Vì
Ta có
Vậy khi d(A; (P)) lớn nhất thì (P) có 1 VTPT
*Phương pháp giải:
- Gọi H, K lần lượt là hình chiếu vuông góc của A lên (P), BC Chứng minh
- Viết phương trình đường thẳng K tham số hóa tọa độ điểm
- Sử dụng tìm tọa độ vectơ
*Cách giải và các dạng bài toán về hệ trục tọa độ trong không gian:
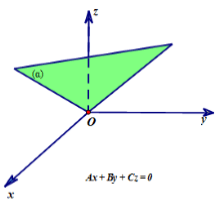
Phương trình tổng quát của mặt phẳng
- Trong không gian Oxy , mọi mặt phẳng đều có dạng phương trình:
Ax + By + Cz + D = 0 với A2 + B2 + C2 ≠ 0
- Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì nó có một VTPT là n→(A; B; C).
- Phương trình mặt phẳng đi qua điểm Mo(xo; yo; zo) và nhận vectơ n→(A; B; C) khác 0→ là VTPT là: A(x - xo) + B(y - yo) + C(z - zo) = 0 .
• Các trường hợp riêng
Xét phương trình mặt phẳng (α): Ax + By + Cz + D = 0 với A2 + B2 + C2 ≠ 0
- Nếu D = 0 thì mặt phẳng (α) đi qua gốc tọa độ O.
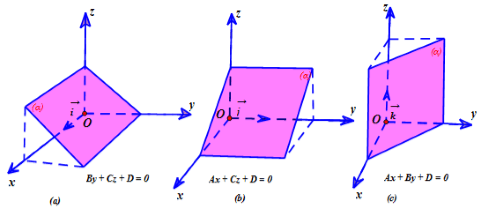
- Nếu A = 0, B ≠ 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Ox.
- Nếu A ≠ 0, B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc chứa trục Oy.
- Nếu A ≠ 0, B ≠ 0, C = 0 thì mặt phẳng (α) song song hoặc chứa trục Oz.
- Nếu A = B = 0, C ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxy).
- Nếu A = C = 0, B ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oxz).
- Nếu B = C = 0, A ≠ 0 thì mặt phẳng (α) song song hoặc trùng với (Oyz).
Chú ý:
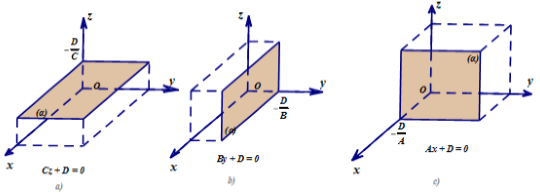
- Nếu trong phương trình (α) không chứa ẩn nào thì (α) song song hoặc chứa trục tương ứng.
- Phương trình mặt phẳng theo đoạn chắn (α): 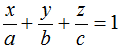
Khoảng cách từ một điểm đến một mặt phẳng.
• Trong không gian Oxyz, cho điểm Mo(xo; yo; zo) và mặt phẳng (α): Ax + By + Cz + D = 0
Khi đó khoảng cách từ điểm Mo đến mặt phẳng (α) được tính:
Góc giữa hai mặt phẳng
Trong không gian Oxyz, cho hai mặt phẳng (α): A1x + B1y + C1z + D1 = 0 và (β): A2x + B2y + C2z + D2 = 0
Góc giữa (α) và (β) bằng hoặc bù với góc giữa hai VTPT nα→, nβ→. Tức là:
Một số dạng bài tập về viết phương trình mặt phẳng
Dạng 1: Viết phương trình mặt phẳng khi biết một điểm và vectơ pháp tuyến của nó.
Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.
Dạng 2: Viết phương trình mặt phẳng (α) đi qua 1 điểm Mo(xo; yo; zo) và song song với 1 mặt phẳng (β): Ax + By + Cz + D = 0 cho trước.
Cách 1: Thực hiện theo các bước sau:
1. VTPT của (β) là nβ→ = (A; B; C)
2. (α) // (β) nên VTPT của mặt phẳng (α) là nα→ = nβ→ = (A; B; C)
3. Phương trình mặt phẳng (α): A(x - x0) + B(y - y0) + C(z - z0) = 0
Cách 2:
1. Mặt phẳng (α) // (β) nên phương trình (P) có dạng: Ax + By + Cz + D' = 0 (*), với D' ≠ D.
2. Vì (P) qua 1 điểm Mo(xo; yo; zo) nên thay tọa độ Mo(xo; yo; zo) vào (*) tìm được D'.
Dạng 3: Viết phương trình mặt phẳng (α) đi qua 3 điểm A, B, C không thẳng hàng.
1. Tìm tọa độ các vectơ: AB→, AC→
2. Vectơ pháp tuyến của (α) là: nα→ = [AB→, AC→]
3. Điểm thuộc mặt phẳng: A (hoặc B hoặc C).
4. Viết phương trình mặt phẳng qua 1 điểm và có VTPT nα
Dạng 4: Viết phương trình mặt phẳng (α) đi qua điểm M và vuông góc với đường thẳng Δ
1. Tìm VTCP của Δ là uΔ→
2. Vì (α) ⊥ Δ nên (α) có VTPT nα→ = uΔ→
3. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT nα→
Dạng 5: Viết phương trình mặt phẳng (α) chứa đường thẳng Δ, vuông góc với mặt phẳng (β)
1. Tìm VTPT của (β) là nβ→
2. Tìm VTCP của Δ là uΔ→
3. VTPT của mặt phẳng (α) là: nα→ = [nβ→; uΔ→]
4. Lấy một điểm M trên Δ
5. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.
Dạng 6: Viết phương trình mặt phẳng (α) qua hai điểm A, B và vuông góc với mặt phẳng (β)
1. Tìm VTPT của (β) là nβ→
2. Tìm tọa độ vectơ AB→
3. VTPT của mặt phẳng (α) là: nα→ = [nβ→, AB→]
4. Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Hệ trục toạ độ trong không gian– Toán lớp 12 Kết nối tri thức
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Xét tất cả các số thực dương a và b thỏa mãn Mệnh đề nào dưới đây đúng?
Xét tất cả các số thực dương a và b thỏa mãn Mệnh đề nào dưới đây đúng?
Câu 2:
Cho hình trụ có chiều cao bằng Cắt hình trụ đã cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng 30. Diện tích xung quanh của hình trụ đã cho bằng:
Cho hình trụ có chiều cao bằng Cắt hình trụ đã cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng 30. Diện tích xung quanh của hình trụ đã cho bằng:
Câu 4:
Cho các số thực dương a, b khác 1 thỏa mãn và ab = 64. Giá trị của biểu thức bằng:
Cho các số thực dương a, b khác 1 thỏa mãn và ab = 64. Giá trị của biểu thức bằng:
Câu 7:
Trong không gian Oxyz, phương trình mặt cầu (S) có tâm I(-1; 2; 1) và đi qua điểm A(0; 4; -1) là:
Trong không gian Oxyz, phương trình mặt cầu (S) có tâm I(-1; 2; 1) và đi qua điểm A(0; 4; -1) là:
Câu 9:
Cho hai số phức là hai nghiệm của phương trình biết Giá trị của biểu thức bằng:
Câu 11:
Cho phương trình (m là tham số thực). Tập hợp tất cả các giá trị m để phương trình đã cho có hai nghiệm phân biệt thuộc [9; 27] là:
Câu 12:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = a, tam giác vuông tại và BC = a (minh họa hình vẽ bên dưới). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
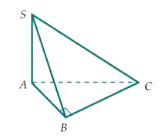
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = a, tam giác vuông tại và BC = a (minh họa hình vẽ bên dưới). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:

Câu 13:
Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng
Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng
Câu 15:
Cho hàm số f(x) liên tục trên bảng xét dấu f'(x) như sau:
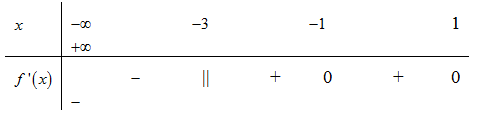
Số điểm cực trị của hàm số đã cho là:

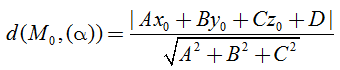
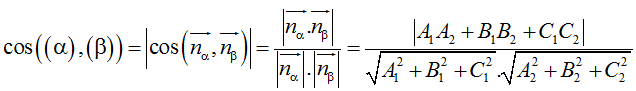


![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)