Câu hỏi:
22/07/2024 315
Nghiệm của phương trình là:
Nghiệm của phương trình là:
A.
B. x = 2
C. x = 3
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
Giải phương trình logarit:
Cách giải:
Chọn C.
Phương pháp:
Giải phương trình logarit:
Cách giải:
Chọn C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Xét tất cả các số thực dương a và b thỏa mãn Mệnh đề nào dưới đây đúng?
Xét tất cả các số thực dương a và b thỏa mãn Mệnh đề nào dưới đây đúng?
Câu 2:
Cho hình trụ có chiều cao bằng Cắt hình trụ đã cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng 30. Diện tích xung quanh của hình trụ đã cho bằng:
Cho hình trụ có chiều cao bằng Cắt hình trụ đã cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng 30. Diện tích xung quanh của hình trụ đã cho bằng:
Câu 3:
Cho các số thực dương a, b khác 1 thỏa mãn và ab = 64. Giá trị của biểu thức bằng:
Cho các số thực dương a, b khác 1 thỏa mãn và ab = 64. Giá trị của biểu thức bằng:
Câu 4:
Trong không gian Oxyz, cho ba điểm Gọi (P) là mặt phẳng chứa BC và cách A một khoảng lớn nhất. Hỏi vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng (P)?
Trong không gian Oxyz, cho ba điểm Gọi (P) là mặt phẳng chứa BC và cách A một khoảng lớn nhất. Hỏi vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng (P)?
Câu 7:
Trong không gian Oxyz, phương trình mặt cầu (S) có tâm I(-1; 2; 1) và đi qua điểm A(0; 4; -1) là:
Trong không gian Oxyz, phương trình mặt cầu (S) có tâm I(-1; 2; 1) và đi qua điểm A(0; 4; -1) là:
Câu 9:
Cho hai số phức là hai nghiệm của phương trình biết Giá trị của biểu thức bằng:
Câu 11:
Cho phương trình (m là tham số thực). Tập hợp tất cả các giá trị m để phương trình đã cho có hai nghiệm phân biệt thuộc [9; 27] là:
Câu 12:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = a, tam giác vuông tại và BC = a (minh họa hình vẽ bên dưới). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
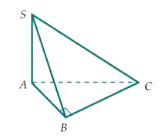
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = a, tam giác vuông tại và BC = a (minh họa hình vẽ bên dưới). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:

Câu 13:
Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng
Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng
Câu 15:
Cho hàm số f(x) liên tục trên bảng xét dấu f'(x) như sau:
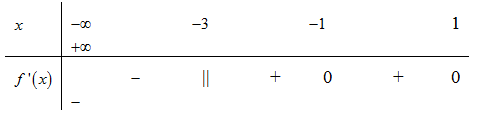
Số điểm cực trị của hàm số đã cho là:



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)