Câu hỏi:
22/11/2024 248Trong các hàm số sau, hàm số nào nghịch biến trên (−∞;+∞)?
A. y=−x4+3x2−2x+1.
B. y=x+12x−2.
C. y=−x3+x2−2x+1.
D. y=x3+3.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là C
Lời giải
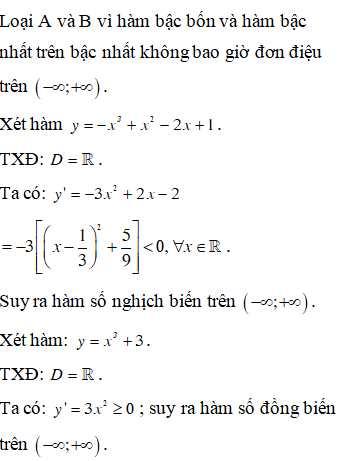
*Phương pháp giải:
Bước 1. Tìm tập xác định D.
Bước 2. Tính đạo hàm y’ = f'(x). Tìm các giá trị xi (i=1, 2, .., n) mà tại đó f'(x) = 0 hoặc f'(x) không xác định.
Bước 4. Sắp xếp các giá trị xi theo thứ tự tăng dần và lập bảng biến thiên.
Bước 5. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số và chọn đáp án chính xác nhất..
*Lý thuyết
1. Định nghĩa.
Cho hàm số y = f(x) xác định trên K, với K là một khoảng, nửa khoảng hoặc một đoạn.
- Hàm số y = f(x) đồng biến (tăng) trên K nếu ∀ x1, x2 ∈ K, x1 < x2 ⇒ f(x1) < f(x2).
- Hàm số y = f(x) nghịch biến (giảm) trên K nếu ∀ x1, x2 ∈ K, x1 < x2 ⇒ f(x1) > f(x2).
2. Điều kiện cần để hàm số đơn điệu.
Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
– Nếu hàm số đồng biến trên khoảng K thì f'(x) ≥ 0, ∀ x ∈ K
– Nếu hàm số nghịch biến trên khoảng K thì f'(x) ≤ 0, ∀ x ∈ K.
3. Điều kiện đủ để hàm số đơn điệu.
Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.
– Nếu f'(x) > 0, ∀x ∈ K thì hàm số đồng biến trên khoảng K.
– Nếu f'(x) < 0, ∀x ∈ K thì hàm số nghịch biến trên khoảng K.
– Nếu f'(x) = 0, ∀x ∈ K thì hàm số không đổi trên khoảng K.
Lưu ý
– Nếu f'(x) ≥ 0, ∀x ∈ K (hoặc f'(x) ≤ 0, ∀x ∈ K) và f'(x) = 0 chỉ tại một số điểm hữu hạn của K thì hàm số đồng biến trên khoảng K (hoặc nghịch biến trên khoảng K).
Xem thêm
TOP 40 câu Trắc nghiệm Sự đồng biến, nghịch biến của hàm số (có đáp án 2024) - Toán 12
Lý thuyết Sự đồng biến, nghịch biến của hàm số (mới 2024 + Bài Tập) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số y = f(x) xác định trên R\{2}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ:
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f(x)=m có 3 nghiệm thực phân biệt.
Câu 2:
Trong trò chơi “Chiếc nón kì diệu” chiếc kim của bánh xe có thể dừng lại ở một trong 7 vị trí với khả năng như nhau. Tính xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau.
Câu 3:
Cho hàm số f(x) liên tục trên đoạn [-1;5] và có đồ thị trên đoạn [-1;5] như hình vẽ bên. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [-1;5] bằng:
Câu 4:
Có bao nhiêu cách mắc nối tiếp 4 bóng đèn được chọn từ 6 bóng đèn khác nhau?
Câu 5:
Cho hàm số y = f(x) có đồ thị như hình vẽ:
Có bao nhiêu giá trị nguyên của m∈(−10;10) để f(√x2+2x+10)−3=m có nghiệm?
Câu 6:
Tìm các giá trị của tham số thực x, y để số phức z=(x+iy)2−2(x+iy)+5 là số thực
Câu 8:
Cho hình nón tròn xoay có đường cao h = 20cm. Gọi 2α là góc ở đỉnh của hình nón với tanα=34. Độ dài đường sinh của hình nón là:
Câu 9:
Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y=|14x4−192x2+30x+m| trên đoạn [0;2] đạt giá trị nhỏ nhất?
Câu 11:
Cho khối lăng trụ đứng ABC.A’B’C’ có BB’=a, đáy ABC là tam giác vuông cân tại B và AC=a√2. Tính thể tích V của khối lăng trụ đã cho.
Câu 13:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB=a, BC=2a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy (ABCD), cạnh SA=a√15. Tính góc tạo bởi đường thẳng SC và mặt phẳng (ABD).
Câu 14:
Biết f(x) là hàm liên tục trên R và 9∫0f(x)dx=9. Khi đó giá trị của 4∫1f(3x−3)dx là:
Câu 15:
Một tỉnh A đưa ra nghị quyết về giảm biên chế cán bộ công chức, viên chức hưởng lương từ ngân sách nhà nước trong giai đoạn 2015-2021 (6 năm) là 10,6% so với số lượng hiện có năm 2015 theo phương thức “ra 2 vào 1” (tức là khi giảm đối tượng hưởng lương từ ngân sách nhà nước 2 người thì được tuyển mới 1 người). Giả sử tỉ lệ giảm và tuyển dụng mới hàng năm so với năm trước đó là như nhau. Tính tỉ lệ tuyển dụng mới hàng năm (làm tròn đến 0,01%).



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)