Câu hỏi:
17/07/2024 65Trong các câu sau đây, câu nào đúng, câu nào sai?
a) Tam giác cân có một góc bằng 60° là tam giác đều.
b) Tam giác cân là tam giác nhọn.
c) Tổng hai góc nhọn của một tam giác vuông bằng 90°.
d) Tam giác vuông cân thì luôn cân tại đỉnh góc vuông và có hai góc nhọn bằng 45°.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
a) Câu a) đúng.
Giải thích:
+ Giả sử tam giác ABC cân tại đỉnh A có góc ở đáy \(\widehat B\) = 60°.
Khi đó, \(\widehat C = \widehat B = 60^\circ \).
Theo định lí tổng ba góc trong tam giác, ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \).
\( \Rightarrow \widehat A = 180^\circ - \widehat B - \widehat C = 180^\circ - 60^\circ - 60^\circ = 60^\circ \).
Do đó, \(\widehat A = \widehat B = \widehat C = 60^\circ \), nên tam giác ABC cân tại đỉnh C.
Vậy tam giác ABC đều.
+ Giả sử tam giác ABC cân tại đỉnh A có góc ở đỉnh \(\widehat A = 60^\circ \).
Theo định lí tổng ba góc trong tam giác, ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \).
Mà \(\widehat B = \widehat C\) (do tam giác ABC cân đỉnh A).
Do đó, \(\widehat B + \widehat B = 180^\circ - \widehat A = 180^\circ - 60^\circ = 120^\circ \), suy ra \(\widehat B = 60^\circ \).
Do đó, \(\widehat A = \widehat B = \widehat C = 60^\circ \), nên tam giác ABC cân tại đỉnh C.
Vậy tam giác ABC đều.
b) Câu b) sai.
Chẳng hạn tam giác ABC cân tại đỉnh A có \(\widehat A = 100^\circ \), \(\widehat B = \widehat C = 40^\circ \), đây là tam giác tù.
c) Từ định lí tổng ba góc trong tam giác, ta suy ra tổng hai góc nhọn của một tam giác vuông bằng 90°.
Vậy câu c) đúng.
d) Tam giác vuông cân thì luôn cân tại đỉnh góc vuông và có hai góc nhọn bằng 45° là câu đúng.
Giả sử có tam giác ABC vuông tại A, cân tại B, khi đó \(\widehat A = \widehat C = 90^\circ \), do đó \(\widehat A + \widehat B + \widehat C > 180^\circ \) không thỏa mãn định lí tổng ba góc trong tam giác.
Vậy tam giác vuông cân thì luôn cân tại đỉnh góc vuông và từ định lí tổng ba góc và tính chất của tam giác cân, ta tính được số đo hai góc nhọn bằng 45°.
Vậy câu a), c), d) đúng và câu b) sai.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
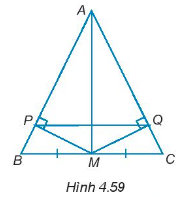
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59).
Đường thẳng PQ có vuông góc với AM không? Vì sao?
Câu 2:
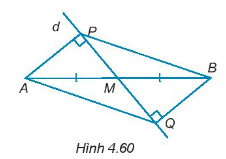
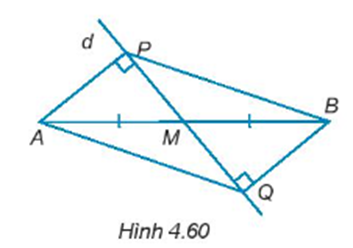
Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P ∈ d, Q ∈ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:
AP = BQ.
Câu 4:
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59).
Chứng minh rằng MP = MQ và AP = AQ.

Câu 5:
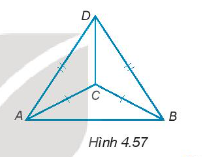
Cho các điểm A, B, C, D như Hình 4.57.
Đường thẳng DC có vuông góc với đường thẳng AB không? Vì sao?
Câu 6:
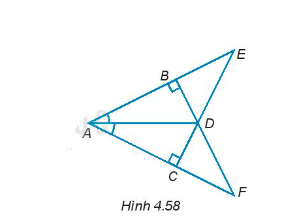
Cho các điểm A, B, C, D, E, F như Hình 4.58.
Chứng minh ∆ADE = ∆ADF.
Câu 7:
Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P ∈ d, Q ∈ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:
∆APB = ∆BQA.
Câu 11:
Cho các điểm A, B, C, D, E, F như Hình 4.58.
Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.

Câu 12:
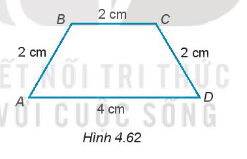
Cho hình thang cân ABCD có đáy lớn AD và đáy nhỏ BC thỏa mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD.