Câu hỏi:
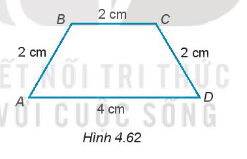
17/07/2024 109Cho hình thang cân ABCD có đáy lớn AD và đáy nhỏ BC thỏa mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Gọi O là trung điểm của AD.
Khi đó, AO = OD = \(\frac{{AD}}{2} = \frac{4}{2} = 2\) (cm).
Do đó, AB = BC = CD = AO = OD = 2 cm.
Tam giác ABO có AB = BO nên tam giác ABO cân tại đỉnh A.
Suy ra \(\widehat {ABO} = \widehat {AOB}\).
Lại có: AD // BC (do ABCD là hình thang cân có AD và BC là đáy)
Suy ra \(\widehat {CBO} = \widehat {AOB}\) (hai góc so le trong).
Do đó, \(\widehat {ABO} = \widehat {AOB} = \widehat {CBO}\).
Xét tam giác ABO và tam giác CBO có:
AB = BC (= 2 cm)
\(\widehat {ABO} = \widehat {CBO}\) (cmt)
BO: cạnh chung
Do đó, ∆ABO = ∆CBO (c – g – c).
Suy ra CO = AO = 2 cm.
Tam giác COD có CD = OD = OC (= 2 cm). Do đó tam giác COD là tam giác đều.
Suy ra \(\widehat D = \widehat {CDO} = 60^\circ \).
Ta có: \(\widehat D + \widehat {BCD} = 180^\circ \) (BC // AD, hai góc ở vị trí trong cùng phía)
Suy ra \(\widehat {BCD} = 180^\circ - \widehat D = 180^\circ - 60^\circ = 120^\circ \).
Do ABCD là hình thang cân với AD và BC là đáy.
Vậy \(\widehat A = \widehat D = 60^\circ \) và \(\widehat {ABC} = \widehat {BCD} = 120^\circ \).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
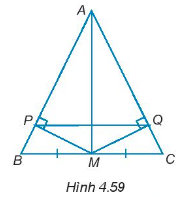
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59).
Đường thẳng PQ có vuông góc với AM không? Vì sao?
Câu 2:
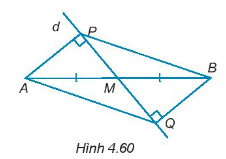
Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P ∈ d, Q ∈ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:
AP = BQ.
Câu 3:
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59).
Chứng minh rằng MP = MQ và AP = AQ.

Câu 5:
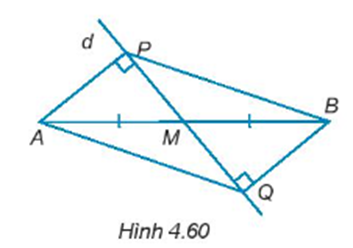
Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P ∈ d, Q ∈ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:
∆APB = ∆BQA.
Câu 6:
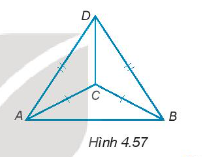
Cho các điểm A, B, C, D như Hình 4.57.
Đường thẳng DC có vuông góc với đường thẳng AB không? Vì sao?
Câu 7:
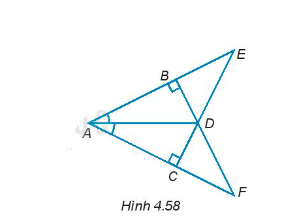
Cho các điểm A, B, C, D, E, F như Hình 4.58.
Chứng minh ∆ADE = ∆ADF.
Câu 11:
Cho các điểm A, B, C, D, E, F như Hình 4.58.
Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.

Câu 12:
Cho các điểm A, B, C, D như Hình 4.57.
Chứng minh rằng \(\widehat {DAC} = \widehat {DBC}\).