Câu hỏi:
19/11/2024 110Thể tích của khối lập phương có độ dài cạnh bằng 6 là
A. 72.
B. 216.
C. 108.
D. 36.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng B
*Lời giải:
Thể tích khối lập phương là
*Phương pháp giải:
- Nắm vững lại kiến thức về hình lập phương: định nghĩa, tính chất, công thức tính S và V
- Thể tích hình lập phương: V = a.a.a =
*Một số lý thuyết và dạng bài tập về hình lập phương:
Hình lập phương là hình hộp chữ nhật có 6 mặt đều là những hình vuông.
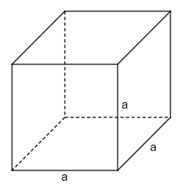
- Thể tích hình lập phương: V = a.a.a =
- Diện tích mỗi mặt của hình lập phương là S = a2
- Diện tích toàn phần (tổng diện tích các mặt) của hình lập phương là Stp = 6a2
- Độ dài đường chéo của hình lập phương là d =
- Độ dài đường chéo mỗi mặt của hình lập phương là
- d(A, (A'BD)) =
- d(A, (CB'D')) =
- d (AC', CD) = d(AC', A'B') =
HÌNH HỘP CHỮ NHẬT
1. Định nghĩa
Hình hộp chữ nhật là một hình không gian có 6 mặt đều là hình chữ nhật.
Hai mặt đối diện nhau của hình chữ nhật được xem là hai mặt đáy của hình chữ nhật. Các mặt còn lại đều là mặt bên của hình chữ nhật.
Hình hộp chữ nhật ba chiều: chiều dài, chiều rộng, chiều cao
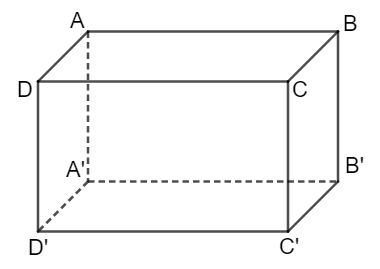
Hình hộp chữ nhật có:
+ 12 cạnh: AB, BC, CD, DA, A’B’, B’C’, C’D’, D’A’, AA’, BB’, CC’, DD’
+ 8 đỉnh: đỉnh A, đỉnh B, đỉnh C, đỉnh D, đỉnh A’, đỉnh B’, đỉnh C, đỉnh D’
+ 6 mặt: ABCD, BCC’B’, A’B’C’D’, DCD’C’, ADD’C’, ABB’A’.
2. Công thức
Cho hình vẽ:
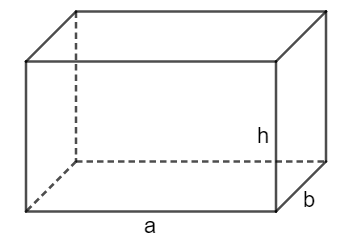
Trong đó:
a: Chiều dài
b: Chiều rộng
h: Chiều cao
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Hình hộp chữ nhật. Hình lập phương (mới 2024 + Bài Tập) - Toán lớp 5
Công thức tính thể tích hình lập phương (chính xác nhất) và cách giải các dạng bài tập
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Chọn ngẫu nhiên ba số từ tập . Xác suất để chọn được ba số mà các số đó lập thành một cấp số nhân tăng có công bội là một số nguyên dương bằng
Câu 2:
Có 8 người cùng vào thang máy của một toà nhà gồm 13 tầng, mỗi người sẽ đi ra ngẫu nhiên ở một trong 13 tầng. Xác suất để mỗi người ra ở một tầng khác nhau bằng
Câu 3:
Có bao nhiêu điểm có toạ độ nguyên nằm trên đường thẳng kẻ được ít nhất hai tiếp tuyến tới đồ thị hàm số .
Câu 4:
Cho hình hộp có tất cả các mặt là hình thoi và các góc đỉnh A bằng (tham khảo hình vẽ bên). Góc giữa hai đường thẳng BD và A′C bằng
Câu 5:
Cho hàm số , với m là tham số thực. Hàm số đã cho có thể có nhiều nhất bao nhiêu điểm cực trị ?
Câu 6:
Cho phương trình có một nghiệm phức . Nghiệm phức còn lại của phương trình là
Câu 7:
Gọi S là tập hợp các số phức z thoả mãn và . Kí hiệu là hai số phức thuộc S và là những số phức có môđun lần lượt nhỏ nhất và lớn nhất. Tính .
Câu 8:
Cho hình lăng trụ tam giác đều ABC.A′B′C’ có (tham khảo hình vẽ bên). Tính khoảng cách giữa hai đường thẳng AB’ và A’C
Câu 10:
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
Câu 11:
Cho hình trụ có MN , PQ vuông góc với nhau lần lượt là hai đường kinh nằm trên hai đường tròn đáy của hình trụ. Thể tích khối tứ diện MNPQ bằng 10. Tính thể tích của khối trụ .
Câu 14:
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm , ,. Mặt phẳng đi qua hai điểm A, B và cách đều hai điểm C, D và hai điểm C, D nằm khác phía so với mặt phẳng . Tính .
Câu 15:
Trong không gian với hệ tọa độ Oxyz, mặt phẳng qua điểm và song song với mặt phẳng toạ độ (Oxy) có phương trình là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)