Câu hỏi:
03/11/2024 1,631Số phức nghịch đảo của số phức z = 1+3i là
A. 110(1−3i)
B. 1−3i
C. 1√10(1+3i)
D. 110(1+3i)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng:A
*Lời giải
ta có số phức z = 1 + 3i
nên ta có 1/z = 1/ 1+3i = 1-3i/10
*Phương pháp giải
- để tìm số phức nghịch đảo của số phức z ta chỉ cần tìm số phức 1/z
*Lý thuyến cần nắm về số phức:
1.1. Số i
Số i là số thỏa mãn: i2 = – 1.
1.2. Định nghĩa số phức
Mỗi biểu thức dạng a + bi , trong đó ; i2 = – 1 được gọi là một số phức.
Đối với số phức z = a + bi, ta nói: a là phần thực, b là phần ảo của z.
Tập hợp các số phức kí hiệu là C.
1.3. Số phức bằng nhau
– Định nghĩa: Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau :
a + bi = c + di a = c và b = d.
– Chú ý :
a) Mỗi số thực a được coi là một số phức với phần ảo bằng 0 : a = a + 0i.
Như vậy, mỗi số thực cũng là một số phức. Ta có:
b) Số phức 0 + bi được gọi là số thuần ảo và viết đơn giản là bi : bi = 0 + bi
Đặc biệt: i = 0 + 1.i
Số i được gọi là đơn vị ảo.
1.4. Biểu diễn hình học số phức
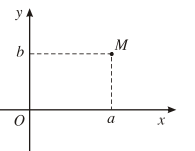
Điểm M(a ; b) trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z = a + bi.
1.5. Môđun của số phức.
Giả sử số phức z = a + bi được biểu diễn bởi điểm M(a ; b) trên mặt phẳng tọa độ.
Độ dài của vecto được gọi là môđun của số phức z và kí hiệu là |z|.
Vậy hay .
Ta thấy:
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Ôn tập chương 4 (mới 2024 + Bài Tập) – Toán 12
190 Bài trắc nghiệm Số phức từ đề thi đại học cực hay có lời giải
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số f(x) thỏa mãn f(1)=3 và f(x)+xf'(x)=4x+1 với mọi x>0. Tính f(2)
Câu 2:
Trong không gian tọa độ Oxyz, mặt phẳng chứa trục Oz và đi qua điểm I(1;2;3) có phương trình là
Câu 3:
Cho hàm số f(x) thỏa mãn f’(x)=27+cosx và f(0)=2019. Mệnh đề nào dưới đây đúng?
Câu 4:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
Câu 5:
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ, biết f(x) đạt cực tiểu tại điểm x=1 và thỏa mãn [f(x)+1] và [f(x)−1] lần lượt chia hết cho (x−1)2 và (x+1)2. Gọi S1,S2 lần lượt là diện tích như trong hình bên. Tính 2S2+8S1
Câu 10:
Cho cấp số cộng (un) với u1 và . Công sai của cấp số cộng đã cho bằng
Câu 12:
Có bao nhiêu số nguyên dương y để tập nghiệm của bất phương trình chứa tối đa 1000 số nguyên.
Câu 14:
Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được khối đá có hình tứ diện MNPQ. Biết rằng MN=60 cm và thể tích khối tứ diện MNPQ bằng Tìm thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân)
Câu 15:
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên. Giá trị cực tiểu của hàm số là số nào sau đây?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)