Đáp án đúng là A

Lời giải

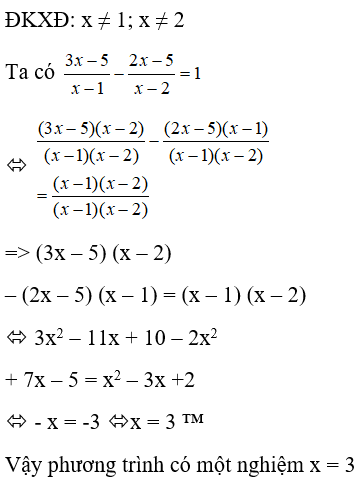
*Phương pháp giải:

Quy đồng khử mẫu đưa về phép tính giải tìm nghiệm

*Lý thuyết:

1. Phép cộng các phân thức đại số

a) Quy tắc cộng hai phân thức cùng mẫu thức

Muốn cộng hai phân thức cùng mẫu thức ta cộng các tử thức với nhau và giữ nguyên mẫu thức (tương tự như cộng hai phân số cùng mẫu).

b) Quy tắc cộng hai phân thức khác mẫu thức

Bước 1: Quy đồng mẫu thức

Bước 2: Cộng hai phân thức cùng mẫu vừa tìm được.

c) Tính chất của phép cộng

Cho ba phân thức $\frac{A}{B};\frac{C}{D};\frac{E}{F}$với $\left(B;D;F\ne 0\right)$

+ Tính giao hoán: $\frac{A}{B}+\frac{C}{D}=\frac{C}{D}+\frac{A}{B}$

+ Tính kết hợp: $\left(\frac{A}{B}+\frac{C}{D}\right)+\frac{E}{F}=\frac{A}{B}+\left(\frac{C}{D}+\frac{E}{F}\right)$

+ Cộng với 0: $\frac{A}{B}+0=0+\frac{A}{B}=\frac{A}{B}$.

2. Phép trừ các phân thức đại số

a) Phân thức đối

- Hai phân thức được gọi là đối nhau nếu tổng của chúng bằng 0.

- Phân thức $\frac{-A}{B}$ là phân thức đối của $\frac{A}{B}$với $\left(B\ne 0\right)$ và ngược lại phân thức $\frac{A}{B}$ là phân thức đối của phân thức $\frac{-A}{B}$. Ta có: $\frac{-A}{B}+\frac{A}{B}=0$.

Như vậy: $-\frac{A}{B}=\frac{-A}{B}$ và $-\frac{-A}{B}=\frac{A}{B}$.

b) Quy tắc trừ hai phân thức đại số

Muốn trừ phân thức $\frac{A}{B}$ cho phân thức $\frac{C}{D}$ ta lấy phân thức $\frac{A}{B}$ cộng với phân thức đối của $\frac{C}{D}$:

$\frac{A}{B}-\frac{C}{D}=\frac{A}{B}+\left(\frac{-C}{D}\right)$ với $\left(B;D\ne 0\right)$.

3. Phép nhân các phân thức đại số

a) Quy tắc nhân phân thức

Muốn nhân hai phân thức ta nhân tử thức với tử thức và mẫu thức với mẫu thức

$\frac{A}{B}.\frac{C}{D}=\frac{AC}{BD}$ với $\left(B;D\ne 0\right)$.

b) Tính chất của phép nhân:

Cho ba phân thức $\frac{A}{B};\frac{C}{D};\frac{E}{F}$với $\left(B;D;F\ne 0\right)$

- Tính giao hoán: $\frac{A}{B}.\frac{C}{D}=\frac{C}{D}.\frac{A}{B}$

- Tính kết hợp: $\left(\frac{A}{B}.\frac{C}{D}\right).\frac{E}{F}=\frac{A}{B}.\left(\frac{C}{D}.\frac{E}{F}\right)$

- Tính phân phối: $\left(\frac{A}{B}+\frac{C}{D}\right).\frac{E}{F}=\frac{A}{B}.\frac{E}{F}+\frac{C}{D}.\frac{E}{F}$

4. Phép chia các phân thức đại số

a) Hai phân thức nghịch đảo

- Hai phân thức nghịch đảo là hai phân thức mà tích của chúng bằng 1.

- Nếu $\frac{A}{B}$ là một phân thức khác 0 thì $\frac{A}{B}.\frac{B}{A}=1$, do đó:

+ Phân thức nghịch đảo của $\frac{A}{B}$là $\frac{B}{A}$.

+ Phân thức nghịch đảo của $\frac{B}{A}$ là $\frac{A}{B}$.

b) Quy tắc chia hai phân thức.

Muốn chia phân thức $\frac{A}{B}$cho phân thức $\frac{C}{D}$ $\left(\frac{C}{D}\ne 0\right)$, ta nhân phân thức $\frac{A}{B}$với nghịch đảo của phân thức $\frac{C}{D}$

Tức là $\frac{A}{B}:\frac{C}{D}=\frac{A}{B}.\frac{D}{C}=\frac{AD}{BC}$$\left(\frac{C}{D}\ne 0\right)$.

Chú ý: Thứ tự thực hiện các phép tính về phân thức cũng giống như thứ tự thực hiện các phép tính về số.

Xem thêm

50 bài tập về phân thức đại số (có đáp án ) – Toán 8 

Lý thuyết Phân thức đại số – Toán lớp 8 Cánh diều