Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
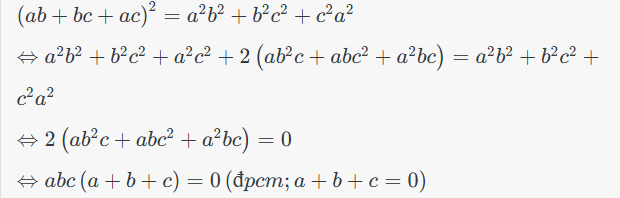
*Phương pháp giải:
Áp dụng bình phương một tổng (A + B)2 = A2 + 2AB + B2.
*Lý thuyết:
1. Bình phương của một tổng
Bình phương của một tổng bằng bình phương số thứ nhất cộng hai lần tích số thứ nhất và số thứ hai cộng bình phương số thứ hai.
Với A, B là các biểu thức tùy ý, ta có: (A + B)2 = A2 + 2AB + B2.
2. Bình phương của một hiệu.
Bình phương của một hiệu bằng bình phương số thứ nhất trừ hai lần tích số thứ nhất và số thứ hai cộng bình phương số thứ hai.
Với A, B là các biểu thức tùy ý, ta có: (A – B)2 = A2 – 2AB + B2.
3. Hiệu hai bình phương
Hiệu hai bình phương bằng tích của hiệu với tổng của chúng.
Với A, B là các biểu thức tùy ý, ta có: A2 – B2 = (A – B)(A + B).
Xem thêm
Lý thuyết Những hằng đẳng thức đáng nhớ (năm + Bài Tập) – Toán 8
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 10:
Cho biểu thức sau B= (n-1) ( n+6) - ( n+1) ( n-6)
Chứng minh rằng B chia hết cho 10 với mọi n thuộc z
Câu 14:
Thực hiện phép tính bằng cách hợp lí nhất
a; (44 . 52 . 60) : (11 . 13 . 15)
b; 123 . 456456 - 456 . 123123
c, 341 . 67 + 341 . 16 + 659 . 83
d; (98 . 7676 - 9898 . 76) : (2001 . 2002 . 2003....2010)


