Câu hỏi:
13/07/2024 269
Nam đo được đường kính của một hình tròn là 24 ± 0,2 cm. Nam tính được chu vi đường tròn là C = 75,36. Hãy ước lượng sai số tuyệt đối của C, biết 3,141 < π < 3,142.
Nam đo được đường kính của một hình tròn là 24 ± 0,2 cm. Nam tính được chu vi đường tròn là C = 75,36. Hãy ước lượng sai số tuyệt đối của C, biết 3,141 < π < 3,142.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi và lần lượt là đường kính và chu vi của đường tròn.
Ta có: 24 – 0,2 ≤ ≤ 24 + 0,2 hay 23,8 ≤ ≤ 24,2
Suy ra 3,141.23,8 ≤ .π ≤ 24,2.3,42 ⇔ 74,7558 ≤ ≤ 76,0364
⇔ 74,7558 – 75,36 ≤ – 75,36 ≤ 76,0364 – 75,36
⇔ – 0,6042 ≤ – 75,36 ≤ 0,6764.
Vậy sai số tuyệt đối của C nằm trong khoảng từ – 0,6042 đển 0,6764.
Gọi và lần lượt là đường kính và chu vi của đường tròn.
Ta có: 24 – 0,2 ≤ ≤ 24 + 0,2 hay 23,8 ≤ ≤ 24,2
Suy ra 3,141.23,8 ≤ .π ≤ 24,2.3,42 ⇔ 74,7558 ≤ ≤ 76,0364
⇔ 74,7558 – 75,36 ≤ – 75,36 ≤ 76,0364 – 75,36
⇔ – 0,6042 ≤ – 75,36 ≤ 0,6764.
Vậy sai số tuyệt đối của C nằm trong khoảng từ – 0,6042 đển 0,6764.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong các hàm số sau, đồ thị của hàm số nhận đường thẳng x = 1 làm trục đối xứng là
Trong các hàm số sau, đồ thị của hàm số nhận đường thẳng x = 1 làm trục đối xứng là
Câu 2:
Một bệnh viện thống kê số ca nhập viện do tai nạn giao thông mỗi ngày trong tháng 9/2020 ở bảng sau:
Số ca
0
1
2
3
4
5
6
7
8
9
12
15
Số ngày
2
3
4
6
3
2
2
3
2
1
1
1
Khoảng tứ phân vị của dãy số liệu trên là:
Một bệnh viện thống kê số ca nhập viện do tai nạn giao thông mỗi ngày trong tháng 9/2020 ở bảng sau:
|
Số ca |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
12 |
15 |
|
Số ngày |
2 |
3 |
4 |
6 |
3 |
2 |
2 |
3 |
2 |
1 |
1 |
1 |
Khoảng tứ phân vị của dãy số liệu trên là:
Câu 3:
Cho tập hợp A = {x ∈ ℝ| – 1 ≤ x < 3}. Xác định phần bù của tập hợp A trong ℝ.
Cho tập hợp A = {x ∈ ℝ| – 1 ≤ x < 3}. Xác định phần bù của tập hợp A trong ℝ.
Câu 4:
Cho định lý “Hai góc đối đỉnh thì bằng nhau”. Mệnh đề nào sau đây đúng
Cho định lý “Hai góc đối đỉnh thì bằng nhau”. Mệnh đề nào sau đây đúng
Câu 5:
Cho hàm số y = x2 – 2x – 2 có đồ thị là parabol (P) và đường thẳng (d) có phương trình y = x + m. Giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B sao cho OA2 + OB2 đạt giá trị nhỏ nhất là:
Cho hàm số y = x2 – 2x – 2 có đồ thị là parabol (P) và đường thẳng (d) có phương trình y = x + m. Giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B sao cho OA2 + OB2 đạt giá trị nhỏ nhất là:
Câu 6:
Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và CD. Đặt , . Hãy phân tích vectơ theo 2 vectơ và :.
Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và CD. Đặt , . Hãy phân tích vectơ theo 2 vectơ và :.
Câu 7:
Cho tam giác ABC đều có cạnh bằng a, gọi H là trung điểm của cạnh BC. Độ dài của vectơ bằng
Câu 8:
Cổng chào Yên Lạc có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng (tính từ mặt đất đến điểm cao nhất của cổng).
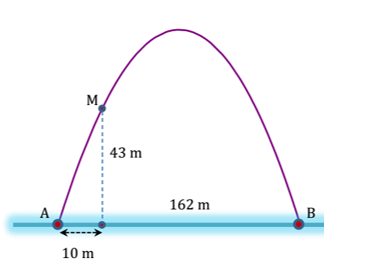
Cổng chào Yên Lạc có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng (tính từ mặt đất đến điểm cao nhất của cổng).

Câu 11:
Cho = 12,096384. Số gần đúng của với độ chính xác d = 0,0004 là:
A. 12,096;
B. 12,09638;
C. 12,0964;
D. 12,10.
Cho = 12,096384. Số gần đúng của với độ chính xác d = 0,0004 là:
A. 12,096;
B. 12,09638;
C. 12,0964;
D. 12,10.
Câu 12:
Cho số gần đúng là a = 1,2357 với độ chính xác là d = 0,01. Số quy tròn của số a là:
Cho số gần đúng là a = 1,2357 với độ chính xác là d = 0,01. Số quy tròn của số a là:
Câu 13:
Cho tam giác ABC có và Gọi I là điểm thỏa mãn Tính độ dài đoạn thẳng AI
Cho tam giác ABC có và Gọi I là điểm thỏa mãn Tính độ dài đoạn thẳng AI
Câu 15:
Để lắp đường dây cao thế từ vị trí A đến vị trí B phải tránh một ngọn núi, do đó người ta phải nối thẳng đường dây từ vị trí A đến vị trí C dài 9 km, rồi nối từ vị trí C đến B dài 12km. Biết góc tạo bởi 2 đoạn dây AC và CB là 52°. Hỏi so với việc nối thẳng từ A đến B phải tốn thêm bao nhiêu mét dây?
Để lắp đường dây cao thế từ vị trí A đến vị trí B phải tránh một ngọn núi, do đó người ta phải nối thẳng đường dây từ vị trí A đến vị trí C dài 9 km, rồi nối từ vị trí C đến B dài 12km. Biết góc tạo bởi 2 đoạn dây AC và CB là 52°. Hỏi so với việc nối thẳng từ A đến B phải tốn thêm bao nhiêu mét dây?


