Câu hỏi:
19/07/2024 126
Có bao nhiêu số phức z đôi một khác nhau thỏa mãn và là số thực?
Có bao nhiêu số phức z đôi một khác nhau thỏa mãn và là số thực?
A. 4
B. 5
C. 7
D. 6
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Từ giả thiết suy ra tập hợp các điểm biểu diễn số phức z
- Từ giả thiết là số thực chứng minh hoặc z - 2 là số thực, hoặc z - 2 là số thuần ảo, hoặc z - 2 có phần thực bằng cộng trừ phần ảo.
- Sử dụng phương pháp hình học.
Cách giải:
Vì nên tập hợp các điểm biểu diễn số phức z là đường tròn tâm I(0; -1), bán kính R = 2.
Gọi ta có:
Vì là số thực nên
TH1: tập hợp các điểm biểu diễn số phức z là đường thẳng x = 2 trừ điểm (2; 0).
TH2: tập hợp các điểm biểu diễn số phức z là đường thẳng y = 0 trừ điểm (-2; 0).
TH3: tập hợp các điểm biểu diễn số phức z là đường thẳng trừ điểm .
Ta có hình vẽ:
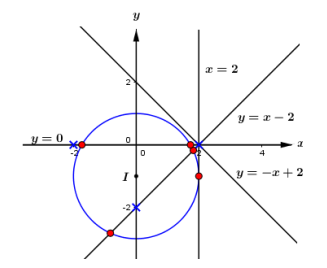
Vậy có 5 số phức z thỏa mãn yêu cầu bài toán.
Chọn B.
Phương pháp:
- Từ giả thiết suy ra tập hợp các điểm biểu diễn số phức z
- Từ giả thiết là số thực chứng minh hoặc z - 2 là số thực, hoặc z - 2 là số thuần ảo, hoặc z - 2 có phần thực bằng cộng trừ phần ảo.
- Sử dụng phương pháp hình học.
Cách giải:
Vì nên tập hợp các điểm biểu diễn số phức z là đường tròn tâm I(0; -1), bán kính R = 2.
Gọi ta có:
Vì là số thực nên
TH1: tập hợp các điểm biểu diễn số phức z là đường thẳng x = 2 trừ điểm (2; 0).
TH2: tập hợp các điểm biểu diễn số phức z là đường thẳng y = 0 trừ điểm (-2; 0).
TH3: tập hợp các điểm biểu diễn số phức z là đường thẳng trừ điểm .
Ta có hình vẽ:

Vậy có 5 số phức z thỏa mãn yêu cầu bài toán.
Chọn B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Một khối trụ có đường cao bằng 2, chu vi thiết diện qua trục gấp 3 lần đường kính đáy. Thể tích của khối trụ đó bằng:
Câu 5:
Có 10 học sinh, gồm 5 bạn lớp 12A và 5 bạn lớp 12B tham gia một trò chơi. Để thực hiện trò chơi, người điều khiển ghép ngẫu nhiên 10 học sinh đó thành 5 cặp. Xác suất để không có cặp nào gồm hai học sinh cùng lớp bằng
Câu 6:
Có bao nhiêu số nguyên a để phương trình có hai nghiệm phức thỏa mãn .
Có bao nhiêu số nguyên a để phương trình có hai nghiệm phức thỏa mãn .
Câu 7:
Giả sử f(x) là một đa thức bậc bốn. Đồ thị hàm số y = f'(1 - x) được cho như hình bên. Hỏi đồ thị hàm số nghịch biến trên khoảng nào trong các khoảng sau?
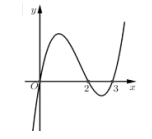

Câu 8:
Giả sử f(x) là một hàm số có đạo hàm liên tục trên Biết rằng là một nguyên hàm của trên Họ tất cả các nguyên hàm của hàm số là:
Câu 9:
Cho đồ thị Đường thẳng d đi qua điểm I(1; 1) cắt (C) tại hai điểm phân biệt A và B. Khi đó diện tích tam giác MAB với M(0; 3) đạt giá trị nhỏ nhất thì độ dài đoạn AB bằng:
Cho đồ thị Đường thẳng d đi qua điểm I(1; 1) cắt (C) tại hai điểm phân biệt A và B. Khi đó diện tích tam giác MAB với M(0; 3) đạt giá trị nhỏ nhất thì độ dài đoạn AB bằng:
Câu 10:
Giả sử f(x) là hàm liên tục trên và diện tích hình phẳng được kẻ sọc ở hình bên bằng 3. Tích phân bằng:
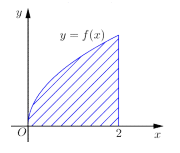
Giả sử f(x) là hàm liên tục trên và diện tích hình phẳng được kẻ sọc ở hình bên bằng 3. Tích phân bằng:

Câu 11:
Cho góc ở đỉnh của một hình nón bằng Gọi r, h, l lần lượt là bán kính đáy, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
Cho góc ở đỉnh của một hình nón bằng Gọi r, h, l lần lượt là bán kính đáy, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
Câu 13:
Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai đường thẳng AB và B'D' bằng:
Câu 14:
Cho hàm số y = f(x) liên tục trên và có bảng xét dấu đạo hàm như hình bên. Hỏi hàm số đã cho có bao nhiêu điểm cực trị?

Cho hàm số y = f(x) liên tục trên và có bảng xét dấu đạo hàm như hình bên. Hỏi hàm số đã cho có bao nhiêu điểm cực trị?




![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)