Câu hỏi:
23/07/2024 2,960
Chứng minh rằng tích các khoảng cách từ một điểm bất kì thuộc hypebol đến hai đường tiệm cận của nó là một số không đổi.
Chứng minh rằng tích các khoảng cách từ một điểm bất kì thuộc hypebol đến hai đường tiệm cận của nó là một số không đổi.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Xét hypebol có phương trình chính tắc là (a > 0, b > 0).
Hai đường tiệm cận của hypebol là: d1 : hay bx + ay = 0 và d2 : hay bx – ay = 0.
Xét điểm M(x; y) bất kì thuộc hypebol. Ta có:
d(M, d1) = , d(M, d2) = .
d(M, d1).d(M, d2) = (*).
Mặt khác, vì M(x; y) thuộc hypebol nên
Thay vào (*) ta được: d(M, d1).d(M, d2) = (không đổi).
Vậy tích các khoảng cách từ một điểm bất kì thuộc hypebol đến hai đường tiệm cận của nó là một số không đổi.
Xét hypebol có phương trình chính tắc là (a > 0, b > 0).
Hai đường tiệm cận của hypebol là: d1 : hay bx + ay = 0 và d2 : hay bx – ay = 0.
Xét điểm M(x; y) bất kì thuộc hypebol. Ta có:
d(M, d1) = , d(M, d2) = .
d(M, d1).d(M, d2) = (*).
Mặt khác, vì M(x; y) thuộc hypebol nên
Thay vào (*) ta được: d(M, d1).d(M, d2) = (không đổi).
Vậy tích các khoảng cách từ một điểm bất kì thuộc hypebol đến hai đường tiệm cận của nó là một số không đổi.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt phẳng toạ độ, hypebol (H) có phương trình chính tắc. Lập phương trình chính tắc của (H) trong mỗi trường hợp sau:
a) (H) có nửa trục thực bằng 4, tiêu cự bằng 10;
b) (H) có tiêu cự bằng , một đường tiệm cận là ;
c) (H) có tâm sai , và đi qua điểm .
Trong mặt phẳng toạ độ, hypebol (H) có phương trình chính tắc. Lập phương trình chính tắc của (H) trong mỗi trường hợp sau:
a) (H) có nửa trục thực bằng 4, tiêu cự bằng 10;
b) (H) có tiêu cự bằng , một đường tiệm cận là ;
c) (H) có tâm sai , và đi qua điểm .
Câu 2:
Cho hypebol .
a) Tìm tiêu cự và độ dài các trục.
b) Tìm các đỉnh và các đường tiệm cận.
Cho hypebol .
a) Tìm tiêu cự và độ dài các trục.
b) Tìm các đỉnh và các đường tiệm cận.
Câu 3:
Trong mặt phẳng toạ độ, cho hypebol có phương trình chính tắc . Tính bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 12.
Trong mặt phẳng toạ độ, cho hypebol có phương trình chính tắc . Tính bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 12.
Câu 4:
Trong mặt phẳng tọa độ, cho hypebol có phương trình chính tắc .
a) Hãy giải thích vì sao nếu điểm M(x0; y0) thuộc hypebol thì các điểm có toạ độ (x0; –y0), (–x0; y0), (–x0; –y0) cũng thuộc hypebol (H.3.12).
b) Tìm toạ độ các giao điểm của hypebol với trục hoành. Hypebol có cắt trục tung hay không? Vì sao?
c) Với điểm M(x0; y0) thuộc hypebol, hãy so sánh |x0| với a.
Trong mặt phẳng tọa độ, cho hypebol có phương trình chính tắc .
a) Hãy giải thích vì sao nếu điểm M(x0; y0) thuộc hypebol thì các điểm có toạ độ (x0; –y0), (–x0; y0), (–x0; –y0) cũng thuộc hypebol (H.3.12).
b) Tìm toạ độ các giao điểm của hypebol với trục hoành. Hypebol có cắt trục tung hay không? Vì sao?
c) Với điểm M(x0; y0) thuộc hypebol, hãy so sánh |x0| với a.
Câu 5:
Một hypebol mà độ dài trục thực bằng độ dài trục ảo được gọi là hypebol vuông. Tìm tâm sai và phương trình hai đường tiệm cận của hypebol vuông.
Một hypebol mà độ dài trục thực bằng độ dài trục ảo được gọi là hypebol vuông. Tìm tâm sai và phương trình hai đường tiệm cận của hypebol vuông.
Câu 6:
Bốn trạm phát tín hiệu vô tuyến có vị trí A, B, C, D theo thứ tự đó thẳng hàng và cách đều với khoảng cách 200 km (H.3.16). Tại một thời điểm, bốn trạm cùng phát tín hiệu với vận tốc 292000 km/s. Một tàu thuỷ nhận được tín hiệu từ trạm C trước 0,0005 s so với tín hiệu từ trạm B và nhận được tín hiệu từ trạm D sớm 0,001 s so với tín hiệu từ trạm A.
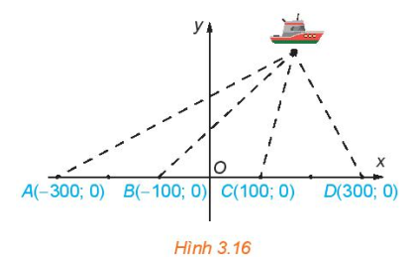
a) Tính hiệu các khoảng cách từ tàu đến các trạm B, C.
b) Tính hiệu các khoảng cách từ tàu đến các trạm A, D.
c) Chọn hệ trục tọa độ Oxy như trong Hình 3.16 (1 đơn vị trên mặt phẳng toạ độ ứng với 100 km trên thực tế). Hãy lập phương trình chính tắc của hai hypebol đi qua vị trí M của tàu. Từ đó, tính toạ độ của M (các số được làm tròn đến hàng đơn vị).
d) Tính các khoảng cách từ tàu đến các trạm B, C (đáp số được làm tròn đến hàng đơn vị, tính theo đơn vị km).
Bốn trạm phát tín hiệu vô tuyến có vị trí A, B, C, D theo thứ tự đó thẳng hàng và cách đều với khoảng cách 200 km (H.3.16). Tại một thời điểm, bốn trạm cùng phát tín hiệu với vận tốc 292000 km/s. Một tàu thuỷ nhận được tín hiệu từ trạm C trước 0,0005 s so với tín hiệu từ trạm B và nhận được tín hiệu từ trạm D sớm 0,001 s so với tín hiệu từ trạm A.
a) Tính hiệu các khoảng cách từ tàu đến các trạm B, C.
b) Tính hiệu các khoảng cách từ tàu đến các trạm A, D.
c) Chọn hệ trục tọa độ Oxy như trong Hình 3.16 (1 đơn vị trên mặt phẳng toạ độ ứng với 100 km trên thực tế). Hãy lập phương trình chính tắc của hai hypebol đi qua vị trí M của tàu. Từ đó, tính toạ độ của M (các số được làm tròn đến hàng đơn vị).
d) Tính các khoảng cách từ tàu đến các trạm B, C (đáp số được làm tròn đến hàng đơn vị, tính theo đơn vị km).
Câu 7:
Một sao chổi đi qua hệ Mặt Trời theo quỹ đạo là một nhánh hypebol nhận tâm Mặt Trời là một tiêu điểm, khoảng cách gần nhất từ sao chổi này đến tâm Mặt Trời là 3.108 km và tâm sai của quỹ đạo hypebol là 3,6 (H.3.15).
Hãy lập phương trình chính tắc của hypebol chứa quỹ đạo, với 1 đơn vị đo trên mặt phẳng toạ độ ứng với 108 km trên thực tế.
Một sao chổi đi qua hệ Mặt Trời theo quỹ đạo là một nhánh hypebol nhận tâm Mặt Trời là một tiêu điểm, khoảng cách gần nhất từ sao chổi này đến tâm Mặt Trời là 3.108 km và tâm sai của quỹ đạo hypebol là 3,6 (H.3.15).
Hãy lập phương trình chính tắc của hypebol chứa quỹ đạo, với 1 đơn vị đo trên mặt phẳng toạ độ ứng với 108 km trên thực tế.
Câu 8:
Cho điểm M(x0; y0) thuộc hypebol có hai tiêu điểm F1(–c; 0), F2(c; 0), độ dài trục thực bằng 2a.
a) Tính MF12 – MF22.
b) Giả sử M(x0; y0) thuộc nhánh chứa đỉnh A2(a; 0), tức là, MF1 – MF2 = 2a. Tính MF1 + MF2, MF1, MF2.
c) Giả sử M(x0; y0) thuộc nhánh chứa đỉnh A1(–a; 0), tức là, MF2 – MF1 = 2a. Tính MF1 + MF2, MF1, MF2.
Cho điểm M(x0; y0) thuộc hypebol có hai tiêu điểm F1(–c; 0), F2(c; 0), độ dài trục thực bằng 2a.
a) Tính MF12 – MF22.
b) Giả sử M(x0; y0) thuộc nhánh chứa đỉnh A2(a; 0), tức là, MF1 – MF2 = 2a. Tính MF1 + MF2, MF1, MF2.
c) Giả sử M(x0; y0) thuộc nhánh chứa đỉnh A1(–a; 0), tức là, MF2 – MF1 = 2a. Tính MF1 + MF2, MF1, MF2.
Câu 9:
Trong mặt phẳng toạ độ, cho hypebol có phương trình chính tắc . Xác định toạ độ các đỉnh, độ dài các trục, tâm sai và phương trình các đường chuẩn của hypebol.
Trong mặt phẳng toạ độ, cho hypebol có phương trình chính tắc . Xác định toạ độ các đỉnh, độ dài các trục, tâm sai và phương trình các đường chuẩn của hypebol.
Câu 10:
Cho hypebol có độ dài trục thực bằng 6, độ dài trục ảo bằng 6 Tính độ dài hai bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 9.
Cho hypebol có độ dài trục thực bằng 6, độ dài trục ảo bằng 6 Tính độ dài hai bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 9.
Câu 11:
Cho hypebol với hai tiêu điểm F1(–2; 0), F2(2; 0). Điểm M nào thuộc hypebol mà có độ dài bán kính tiêu MF2 nhỏ nhất? Tính khoảng cách từ điểm đó tới các tiêu điểm.
Cho hypebol với hai tiêu điểm F1(–2; 0), F2(2; 0). Điểm M nào thuộc hypebol mà có độ dài bán kính tiêu MF2 nhỏ nhất? Tính khoảng cách từ điểm đó tới các tiêu điểm.
Câu 12:
Cho hypebol có phương trình chính tắc với các tiêu điểm F1(–c; 0), F2(c; 0). Xét các đường thẳng và (H.3.14). Với điểm M(x; y) thuộc hypebol, tính các tỉ số và theo a và c.
Cho hypebol có phương trình chính tắc với các tiêu điểm F1(–c; 0), F2(c; 0). Xét các đường thẳng và (H.3.14). Với điểm M(x; y) thuộc hypebol, tính các tỉ số và theo a và c.
Câu 13:
Trong mặt phẳng toạ độ Oxy, hypebol (H) có phương trình chính tắc, có tâm sai e = 2 và một đường chuẩn là x = 8. Lập phương trình chính tắc của (H).
Trong mặt phẳng toạ độ Oxy, hypebol (H) có phương trình chính tắc, có tâm sai e = 2 và một đường chuẩn là x = 8. Lập phương trình chính tắc của (H).


