Câu hỏi:
17/06/2026 3,389
Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tâm của hai tam giác ABD và ACD. Chứng minh G1G2 song song với các mặt phẳng (ABC) và (BCD).
Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tâm của hai tam giác ABD và ACD. Chứng minh G1G2 song song với các mặt phẳng (ABC) và (BCD).
Trả lời:
Giải bởi Vietjack
*Lời giải
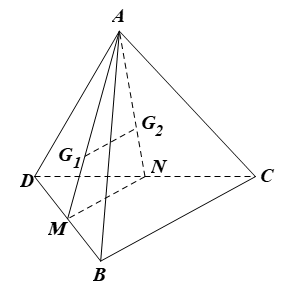
Gọi M, N lần lượt là trung điểm của DB, DC.
Xét ∆DBC có M, N lần lượt là trung điểm của DB, DC nên MN là đường trung bình của ∆DBC, suy ra MN // BC.
Do G1 là trọng tâm ∆ABD nên
G2 là trọng tâm ∆ACD nên
Do đó
Trong tam giác AMN, ta có nên G1G2 // MN (định lí Thalès đảo)
Mà MN // BC (chứng minh trên)
Suy ra G1G2 // MN // BC, mà BC ⊂ (ABC), MN ⊂ (BCD).
Suy ra G1G2 song song với các mặt phẳng (ABC) và (BCD).
*Phương pháp giải
Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).
*Lý thuyết cần nắm thêm về đường thẳng và mặt phẳng song song
Cho đường thẳng d và mặt phẳng (α). Tùy theo số điểm chung của d và (α), ta có ba trường hợp sau:
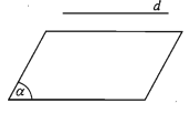
- d và (α) không có điểm chung. Khi đó ta nói d song song với (α) hay (α) song song với d và kí hiệu là d // (α) hay (α) // d.
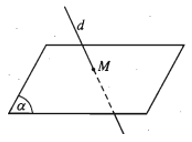
- d và (α) chỉ có một điểm chung duy nhất M. Khi đó ta nói d và (α) cắt nhau tại điểm M và kí hiệu .
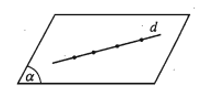
- d và (α) có từ hai điểm chung trở lên. Khi đó, d nằm trong (α) hay (α) chứa d và kí hiệu .
II. Tính chất
- Định lí. Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d’ nằm trong (α) thì d song song với (α).
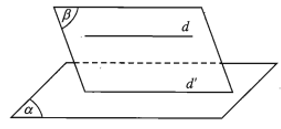
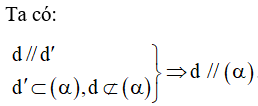
- Định lí. Cho đường thẳng a song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa a và cắt (α) theo giao tuyến b thì b song song với a.
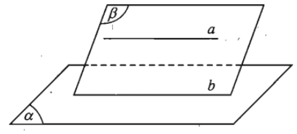
- Hệ quả. Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
- Định lí. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Xem thêm một số bài viết liên quan hay, chi tiết:
Lý thuyết Đường thẳng và mặt phẳng song song (mới + Bài Tập) - Toán 11
Gọi M, N lần lượt là trung điểm của DB, DC.
Xét ∆DBC có M, N lần lượt là trung điểm của DB, DC nên MN là đường trung bình của ∆DBC, suy ra MN // BC.
Do G1 là trọng tâm ∆ABD nên
G2 là trọng tâm ∆ACD nên
Do đó
Trong tam giác AMN, ta có nên G1G2 // MN (định lí Thalès đảo)
Mà MN // BC (chứng minh trên)
Suy ra G1G2 // MN // BC, mà BC ⊂ (ABC), MN ⊂ (BCD).
Suy ra G1G2 song song với các mặt phẳng (ABC) và (BCD).
*Phương pháp giải
Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).
*Lý thuyết cần nắm thêm về đường thẳng và mặt phẳng song song
Cho đường thẳng d và mặt phẳng (α). Tùy theo số điểm chung của d và (α), ta có ba trường hợp sau:
- d và (α) không có điểm chung. Khi đó ta nói d song song với (α) hay (α) song song với d và kí hiệu là d // (α) hay (α) // d.
- d và (α) chỉ có một điểm chung duy nhất M. Khi đó ta nói d và (α) cắt nhau tại điểm M và kí hiệu .
- d và (α) có từ hai điểm chung trở lên. Khi đó, d nằm trong (α) hay (α) chứa d và kí hiệu .
II. Tính chất
- Định lí. Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d’ nằm trong (α) thì d song song với (α).
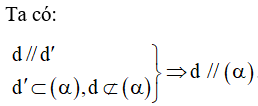
- Định lí. Cho đường thẳng a song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa a và cắt (α) theo giao tuyến b thì b song song với a.
- Hệ quả. Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
- Định lí. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Xem thêm một số bài viết liên quan hay, chi tiết:
Lý thuyết Đường thẳng và mặt phẳng song song (mới + Bài Tập) - Toán 11
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi (α) là mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA. Tìm giao tuyến của mặt phẳng (α) với các mặt của hình chóp.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi (α) là mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA. Tìm giao tuyến của mặt phẳng (α) với các mặt của hình chóp.
Câu 2:
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’.
a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE).
b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho Chứng minh MN // (DCEF).
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’.
a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE).
b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho Chứng minh MN // (DCEF).
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi G là trọng tâm của tam giác SAB, I là trung điểm của AB và M là điểm thuộc cạnh AD sao cho Đường thẳng đi qua M và song song với AB cắt CI tại N. Chứng minh:
a) NG // (SCD);
b) MG // (SCD).
Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của hai cạnh AB và CD, P là trung điểm của SA. Chứng minh:
a) MN song song với các mặt phẳng (SBC) và (SAD);
b) SB song song với (MNP);
c) SC song song với (MNP).
d) Gọi G1 và G2 theo thứ tự là trọng tâm của hai tam giác ABC và SBC. Chứng minh G1G2 song song với (SAD).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của hai cạnh AB và CD, P là trung điểm của SA. Chứng minh:
a) MN song song với các mặt phẳng (SBC) và (SAD);
b) SB song song với (MNP);
c) SC song song với (MNP).
d) Gọi G1 và G2 theo thứ tự là trọng tâm của hai tam giác ABC và SBC. Chứng minh G1G2 song song với (SAD).
