Cho tam giác ABC đều cạnh a. Mệnh đề nào sau đây đúng?

Đáp án đúng là: C

*Lời giải

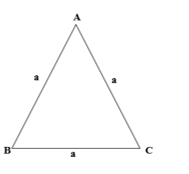
Độ dài các cạnh của tam giác là a thì độ dài các vectơ

*Phương pháp giải

-Độ dài đoạn thẳng AB được gọi là độ dài vecto AB, kí hiệu $\left|\overrightarrow{AB}\right|$. Vậy AB = $\left|\overrightarrow{AB}\right|$.

-Hai vecto bằng nhau khi chúng cùng hướng và cùng độ dài.

-Hai vecto đối nhau nếu chúng ngược hướng và cùng độ dài.

*Một số lý thuyết nắm thêm về vectơ trong không gian:

I. Định nghĩa và các phép toán về vecto trong không gian.

Cho đoạn thẳng AB trong không gian. Nếu ta chọn điểm đầu là A, điểm cuối là B ta có một vecto, được kí hiệu là $\overrightarrow{AB}$.

1. Định nghĩa.

- Vecto trong không gian là một đoạn thẳng có hướng. Kí hiệu $\overrightarrow{AB}$ chỉ vecto có điểm đầu là A, điểm cuối là B. Vecto còn được kí hiệu là $\overrightarrow{a};\overrightarrow{b};\overrightarrow{x};\overrightarrow{y}\mathrm{....}$

- Các khái niệm liên quan đến vecto như giá của vecto, độ dài của vecto, sự cùng phương, cùng hướng của vecto, vecto – không, sự bằng nhau của hai vecto … được định nghĩa tương tự như trong mặt phẳng.

2. Phép cộng và phép trừ vecto trong không gian

- Phép cộng và phép trừ của hai vecto trong không gian được định nghĩa tương tự như phép cộng và phép trừ hai vecto trong mặt phẳng.

- Phép cộng vecto trong không gian cũng có các tính chất như phép cộng vecto trong mặt phẳng. Khi thực hiện phép cộng vecto trong không gian ta vẫn có thể áp dụng quy tắc ba điểm, quy tắc hình bình hành như đối với vecto trong hình học phẳng.

II. Điều kiện đồng phẳng của ba vecto.

1. Khái niệm về sự đồng phẳng của ba vecto trong không gian.

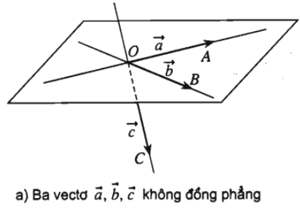
Trong không gian cho ba vecto $\overrightarrow{a};\overrightarrow{b};\overrightarrow{c}\ne \overrightarrow{0}$. Nếu từ một điểm O bất kì ta vẽ: $\overrightarrow{OA}=\overrightarrow{a};\overrightarrow{OB}=\overrightarrow{b};\overrightarrow{OC}=\overrightarrow{c}$ thì có thể xảy ra hai trường hợp:

+ Trường hợp các đường thẳng OA; OB; OC không cùng nằm trong một mặt phẳng, khi đó ta nói rằng ba vecto $\overrightarrow{a};\overrightarrow{b};\overrightarrow{c}$ không đồng phẳng.

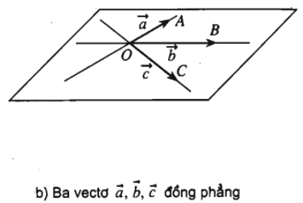
+ Trường hợp các đường thẳng OA; OB; OC cùng nằm trong một mặt phẳng thì ta nói rằng ba vecto $\overrightarrow{a};\overrightarrow{b};\overrightarrow{c}$ đồng phẳng.

Trong trường hợp này, giá của các vecto $\overrightarrow{a};\overrightarrow{b};\overrightarrow{c}$ luôn luôn song song với một mặt phẳng.

- Chú ý. Việc xác định sự đồng phẳng hoặc không đồng phẳng của ba vecto nói trên không phụ thuộc vào việc chọn điểm O.

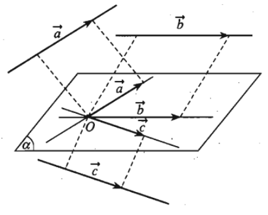
2. Định nghĩa:

Trong không gian ba vecto được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.

3. Điều kiện để ba vecto đồng phẳng.

- Định lí 1.

Trong không gian cho hai vecto $\overrightarrow{a};\overrightarrow{b}$ không cùng phương và vecto $\overrightarrow{c}$. Khi đó, ba vecto $\overrightarrow{a};\overrightarrow{b};\overrightarrow{c}$ đồng phẳng khi và chỉ khi có cặp số m; n sao cho $\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}$. Ngoài ra, cặp số m; n là suy nhất.

- Định lí 2.

Trong không gian cho ba vecto không đồng phẳng $\overrightarrow{a};\overrightarrow{b};\overrightarrow{c}$. Khi đó, với mọi vecto ta đều tìm được một bộ ba số m, n, p sao cho $\overrightarrow{x}=m\overrightarrow{a}+n\overrightarrow{b}+p\overrightarrow{c}$. Ngoài ra, bộ ba số m; n; p là duy nhất.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Vectơ trong không gian (mới 2024 + Bài Tập) - Toán 11

50 Bài tập Vectơ trong không gian Toán 11 mới nhất 

80 câu trắc nghiệm Vectơ cơ bản