Câu hỏi:
09/11/2024 1,173Cho bốn điểm bất kì A; B; C; D. Mệnh đề nào sau đây đúng?
A 
B 
C 
D 
Trả lời:
Giải bởi Vietjack
Đáp án đúng là:A
Lời giải
*Phương pháp giải:
Sử dụng quy tắc ba điểm, quy tắc hình bình hành, trung điểm, trọng tâm, để biến đổi vế này thành vế kia của đẳng thức hoặc biến đổi cả hai vế để được hai vế bằng nhau hoặc ta cũng có thể biến đổi đẳng thức véctơ cần chứng minh đó tương đương với một đẳng thức vectơ đã được công nhận là đúng.
*Lý thuyết:
- Tổng của hai vectơ: Cho hai vectơ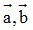 
tùy ý. Lấy một điểm A tùy ý, vẽ vectơ
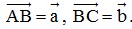Vectơ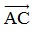
được gọi là tổng của hai vectơ 
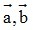tức là: 
.
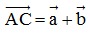- Tính chất của phép cộng các vectơ: Với các vectơ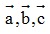
tùy ý ta có:
+) 
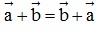(tính chất giao hoán);
+) 
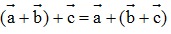(tính chất kết hợp);
+) 
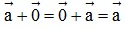(tính chất của vectơ – không)
- Vectơ đối: Vectơ có cùng độ dài và ngược hướng với vectơ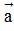
được gọi là vectơ đối của vectơ 
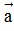. Kí hiệu là -
.
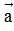- Hiệu của hai vectơ: Cho hai vectơ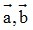 
tùy ý. Ta có: 
.
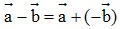- Quy tắc ba điểm: Với A, B, C tùy ý ta luôn có: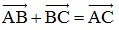 
và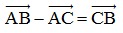
- Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì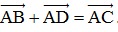 
.
- Quy tắc trung điểm: Với I là trung điểm của đoạn thẳng AB ⇔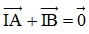 
.
- Quy tắc trọng tâm: Với G là trọng tâm của tam giác ABC ⇔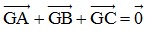 
.
- Chú ý: Vectơ đối của vectơ - không là vectơ - không.
Xem thêm
Lý thuyết Biểu thức tọa độ của các phép toán vectơ chi tiết – Toán lớp 10 Cánh diều
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào sau đây đúng?
Câu 3:
Cho tam giác ABC, với M là trung điểm BC. Mệnh đề nào sau đây đúng?
Câu 5:
Cho M; N; P lần lượt là trung điểm các cạnh AB; BC; CA của tam giác ABC Hỏi vectơ bằng vectơ nào?
Câu 6:
Cho đường tròn tâm O và hai tiếp tuyến MT và MT’ (T và T’ là hai tiếp điểm). Khẳng định nào sau đây đúng?
Câu 7:
Cho đường tròn tâm O và hai tiếp tuyến song song với nhau tiếp xúc với đường tròn tại hai điểm A và B.Mệnh đề nào sau đây đúng?
Câu 9:
Cho tam giác ABC, với M; N ; P lần lượt là trung điểm của BC; CA; AB. Khẳng định nào sau đây sai?
Câu 12:
Cho tam giác ABC cân tại A và đường cao AH. Đẳng thức nào sau đây đúng?
Câu 14:
Cho lục giác đều ABCDEF tâm O . Hỏi có bao nhiêu vecto khác vecto không ; cùng phương với có điểm đầu và điểm cuối là các đỉnh của lục giác?
Câu 15:
Cho tứ giác ABCD. Có bao nhiêu vectơ khác vectơ không có điểm đầu và cuối là các đỉnh của tứ giác?
