Câu hỏi:
19/07/2024 408Cho tam giác ABC có AB = c, BC = a và AC = b. Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Trong các mệnh đề sau, mệnh đề nào sai?
A. \(\frac{a}{{\sin A}} = 2R;\)
B. 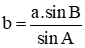 .
.
C. b = 2R.sinA;
D. c = 2R.sinC.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Theo định lí sin ta có: \[\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\] Do đó A đúng.
Từ \[\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\] ta suy ra \(b = \frac{a}{{\sin A}}.\sin B = \frac{{a.\sin B}}{{\sin A}}.\) Do đó B đúng.
Ta cũng có hệ quả định lí sin: b = 2R.sinB và c = 2R.sinC.
Do đó C sai và D đúng.
Vậy ta chọn phương án C.
Hướng dẫn giải
Đáp án đúng là: C
Theo định lí sin ta có: \[\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\] Do đó A đúng.
Từ \[\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\] ta suy ra \(b = \frac{a}{{\sin A}}.\sin B = \frac{{a.\sin B}}{{\sin A}}.\) Do đó B đúng.
Ta cũng có hệ quả định lí sin: b = 2R.sinB và c = 2R.sinC.
Do đó C sai và D đúng.
Vậy ta chọn phương án C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác; p, S lần lượt là nửa chu vi và diện tích tam giác. Khẳng định nào sau đây là đúng?
Câu 2:
Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Đẳng thức nào đúng?
Câu 3:
Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Công thức tính diện tích tam giác ABC nào sau đây là đúng:
Câu 4:
Cho tam giác ABC có BC = a, AC = b và AB = c. Biết \(\widehat C = 120^\circ .\) Khẳng định nào sau đây là đúng?
Câu 5:
Cho tam giác ABC có \[\frac{{{b^2} + {c^2}--{a^2}}}{{2bc}} > 0\]. Khi đó:


