Câu hỏi:
30/10/2024 223
Cho khối lăng trụ đứng ABC.A'B'C' có BB' = a, đáy ABC là tam giác vuông cân tại B và AB = a. Tính thể tích V của khối lăng trụ đã cho.
Cho khối lăng trụ đứng ABC.A'B'C' có BB' = a, đáy ABC là tam giác vuông cân tại B và AB = a. Tính thể tích V của khối lăng trụ đã cho.
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: D
*Lời giải
Thể tích V của khối lăng trụ đã cho là
*Phương pháp giải
- áp dụng công thức tính thể tích lăng trụ đứng tam giác: V = B.h, với đáy là tam giác vuông cân tại B có AB=a; chiều cao BB' = a
*Các dạng bài về hình lăng trụ đứng tam giác
a) Nhận biết các yếu tố của lăng trụ đứng tam giác, tứ giác
*Phương pháp: vẽ hình, quan sát để xác định các mặt, các cạnh, các đỉnh.Để vẽ hình lăng trụ đứng, ta thường vẽ một đáy, sau đó vẽ các cạnh bên là các đoạn thẳng song song và bằng nhau.
b) Tính diện tích, thể tích của hình lăng trụ đứng tam giác, tứ giác
*) lăng trụ đứng tam giác:
+ Diện tích xung quanh của hình lăng trụ đứng tam giác bằng tích của chu vi đáy với chiều cao của nó.
+ Diện tích toàn phần: Diện tích toàn phần bằng diện tích xung quanh cộng diện tích hai đáy.
+ Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.
*) lăng trụ đứng tứ giác:
+ Diện tích xung quanh của hình lăng trụ đứng tứ giác bằng tích của chu vi đáy với chiều cao của nó.
+ Diện tích toàn phần: Diện tích toàn phần bằng diện tích xung quanh cộng diện tích hai đáy.
+ Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.
+) Khối lăng trụ đều là khối lăng trụ có đáy là tam giác đều.
+ Tính diện tích đáy, chiều cao hình lăng trụ.
+ Tính thể tích khối lăng trụ.
+ Chú ý: Diện tích tam giác đều cạnh a là 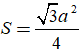
Diện tích hình vuông cạnh a: S= a2.
PHƯƠNG PHÁP TÍNH THỂ TÍCH LĂNG TRỤ
Bước 1: Xác định và tính chiều cao của khối đa diện
Bước 2: Tìm diện tích đáy bằng các công thức.
Bước 3: Sử dụng công thức tính thể tích
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Ôn tập chương 1 – Toán 12
Bài toán về thể tích khối lăng trụ (có đáp án) – Toán 12
Trắc nghiệm Khái niệm về thể tích của khối đa diện (có đáp án) - Toán 12
Đáp án đúng: D
*Lời giải
Thể tích V của khối lăng trụ đã cho là*Các dạng bài về hình lăng trụ đứng tam giác
a) Nhận biết các yếu tố của lăng trụ đứng tam giác, tứ giác
*Phương pháp: vẽ hình, quan sát để xác định các mặt, các cạnh, các đỉnh.Để vẽ hình lăng trụ đứng, ta thường vẽ một đáy, sau đó vẽ các cạnh bên là các đoạn thẳng song song và bằng nhau.
b) Tính diện tích, thể tích của hình lăng trụ đứng tam giác, tứ giác
*) lăng trụ đứng tam giác:
+ Diện tích xung quanh của hình lăng trụ đứng tam giác bằng tích của chu vi đáy với chiều cao của nó.
+ Diện tích toàn phần: Diện tích toàn phần bằng diện tích xung quanh cộng diện tích hai đáy.
+ Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.
*) lăng trụ đứng tứ giác:
+ Diện tích xung quanh của hình lăng trụ đứng tứ giác bằng tích của chu vi đáy với chiều cao của nó.
+ Diện tích toàn phần: Diện tích toàn phần bằng diện tích xung quanh cộng diện tích hai đáy.
+ Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.
+) Khối lăng trụ đều là khối lăng trụ có đáy là tam giác đều.
+ Tính diện tích đáy, chiều cao hình lăng trụ.
+ Tính thể tích khối lăng trụ.
+ Chú ý: Diện tích tam giác đều cạnh a là
Diện tích hình vuông cạnh a: S= a2.
PHƯƠNG PHÁP TÍNH THỂ TÍCH LĂNG TRỤ
Bước 1: Xác định và tính chiều cao của khối đa diện
Bước 2: Tìm diện tích đáy bằng các công thức.
Bước 3: Sử dụng công thức tính thể tích
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Ôn tập chương 1 – Toán 12
Bài toán về thể tích khối lăng trụ (có đáp án) – Toán 12
Trắc nghiệm Khái niệm về thể tích của khối đa diện (có đáp án) - Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số có đồ thị là đường cong trong hình bên. Giá trị của biểu thức T = f(2) - f(0) bằng
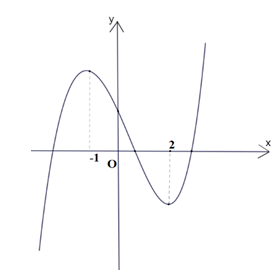
Cho hàm số có đồ thị là đường cong trong hình bên. Giá trị của biểu thức T = f(2) - f(0) bằng

Câu 2:
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số để hàm số nghịch biến trên khoảng (0;1)?
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số để hàm số nghịch biến trên khoảng (0;1)?
Câu 3:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng . Gọi M, N lần lượt là trung điểm của SB, SC. Biết mặt phẳng (AMN) vuông góc với mặt phẳng (SBC). Tính thể tích của khối chóp A.BCNM .
Câu 4:
Cho khối chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, , cạnh bên SA vuông góc với đáy, mặt bên (SCD) tạo với đáy một góc 60o. Thể tích khối chóp S.ABCD bằng
Cho khối chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, , cạnh bên SA vuông góc với đáy, mặt bên (SCD) tạo với đáy một góc 60o. Thể tích khối chóp S.ABCD bằng
Câu 5:
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
![Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số g(x) = 2f(x) - 1 trên đoạn [-1;2] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/03/blobid6-1680192072.png)
Giá trị lớn nhất của hàm số g(x) = 2f(x) - 1 trên đoạn [-1;2] là
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
![Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số g(x) = 2f(x) - 1 trên đoạn [-1;2] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/03/blobid6-1680192072.png)
Giá trị lớn nhất của hàm số g(x) = 2f(x) - 1 trên đoạn [-1;2] là
Câu 6:
Cho phương trình Tìm tất cả các giá trị của tham số m để phương trình (1) có ba nghiệm thỏa mãn
Cho phương trình Tìm tất cả các giá trị của tham số m để phương trình (1) có ba nghiệm thỏa mãn
Câu 7:
Cho hàm số , với có đồ thị tiếp xúc trục hoành tại điểm có hoành độ bằng 1 và cắt đường thẳng tại hai điểm phân biệt có hoành độ lần lượt là 0 và 4, với m là tham số. Số nghiệm của phương trình f(x) = f(-3) là.
Câu 8:
Cho hình chóp S.ABC có AB vuông góc với mặt phẳng (ABC) và SA = a. Tam giác ABC có . Tính số đo góc giữa đường thẳng SB và mặt phẳng (ABC)
Cho hình chóp S.ABC có AB vuông góc với mặt phẳng (ABC) và SA = a. Tam giác ABC có . Tính số đo góc giữa đường thẳng SB và mặt phẳng (ABC)
Câu 9:
Cho hàm số y = f(x). Hàm số y = f'(x) có bảng biến thiên như sau:
![Cho hàm số y = f(x). Hàm số y = f'(x) có bảng biến thiên như sau: Điều kiện cần và đủ của tham số m để bất phương trình f(x) - 1/2x^2 < m nghiệm đúng với mọi x thuộc [1;2] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/03/blobid8-1680205280.png)
Điều kiện cần và đủ của tham số m để bất phương trình nghiệm đúng với mọi là
Cho hàm số y = f(x). Hàm số y = f'(x) có bảng biến thiên như sau:
![Cho hàm số y = f(x). Hàm số y = f'(x) có bảng biến thiên như sau: Điều kiện cần và đủ của tham số m để bất phương trình f(x) - 1/2x^2 < m nghiệm đúng với mọi x thuộc [1;2] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/03/blobid8-1680205280.png)
Điều kiện cần và đủ của tham số m để bất phương trình nghiệm đúng với mọi là
Câu 10:
Cho khối hộp chữ nhật có hai kích thước là 2; 3 và độ dài đường chéo bằng 5. Thể tích khối hôp đã cho bằng
Cho khối hộp chữ nhật có hai kích thước là 2; 3 và độ dài đường chéo bằng 5. Thể tích khối hôp đã cho bằng
Câu 11:
Có bao nhiêu giá trị thực của tham số m để tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;1] bằng -1 ?
Có bao nhiêu giá trị thực của tham số m để tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;1] bằng -1 ?
Câu 12:
Cho hàm số có đồ thị là đường cong trong hình bên. Dấu của các hệ số thực a, b, c là
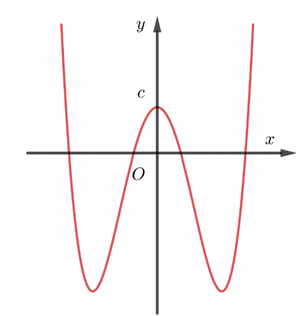
Cho hàm số có đồ thị là đường cong trong hình bên. Dấu của các hệ số thực a, b, c là

Câu 13:
Cho hàm số có đồ thị là đường cong trong hình bên. Hàm số y = f(-x) nghịch biến trong khoảng nào dưới đây?
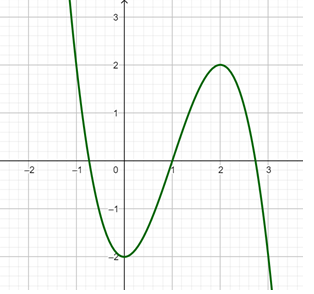
Cho hàm số có đồ thị là đường cong trong hình bên. Hàm số y = f(-x) nghịch biến trong khoảng nào dưới đây?

Câu 14:
Tìm tất cả các giá trị của tham số m để đồ thị hàm số có đúng một điểm cực đại.
Tìm tất cả các giá trị của tham số m để đồ thị hàm số có đúng một điểm cực đại.
Câu 15:
Cho hàm số với và có bảng biến thiên như sau:
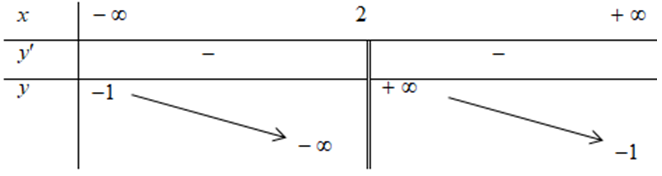
Giá trị của a + b là
Cho hàm số với và có bảng biến thiên như sau:

Giá trị của a + b là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)