Câu hỏi:
05/11/2024 1,157Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB=3a, BC=4a, SA=12a và SA vuông góc với đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD
A. R=13a2
B. R=6a
C. R=5a2
D. R=17a2
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A.
*Lời giải:
* Gọi O là tâm của hình chữ nhật ABCD. Dựng đường thẳng Ox vuông góc mặt phẳng đáy, ta có Ox//SA⇒Ox∩SC=I. Dễ thấy, I là trung điểm của SC cách đều các đỉnh S,A,C và là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD ta có R=SC2.
* Xét tam giác ABC:AC=√AB2+BC2=√9a2+16a2=5a.
Xét tam giác SAC:SC=√SA2+AC2=√144a2+25a2=13a.
Vậy R=SC2=13a2.
Mặt cầu ngoại tiếp hình chóp.
+ Xác định trục d của đường tròn ngoại tiếp đa giác đáy (d là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).
+ Xác định mặt phẳng trung trực (P) của một cạnh bên (hoặc trục Δ của của đường tròn ngoại tiếp một đa giác của mặt bên).
+ Giao điểm I của (P) và d (hoặc của Δ và d ) là tâm mặt cầu ngoại tiếp.
+ Kết luận: I là tâm mặt cầu ngoại tiếp chóp.
Nhận xét: Hình chóp có đáy hoặc các mặt bên là các đa giác không nội tiếp được đường tròn thì hình chóp đó không nội tiếp được mặt cầu.
Cách xác định tâm và bán kính mặt cầu ngoại tiếp của một số hình đa diện cơ bản
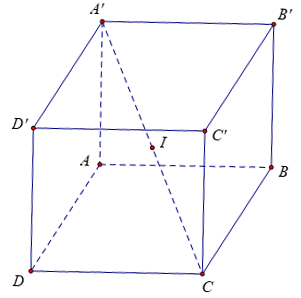
a/ Hình hộp chữ nhật, hình lập phương.
- Tâm: trùng với tâm đối xứng của hình hộp chữ nhật (hình lập phương).
⇒ Tâm là I, là trung điểm của AC'.
- Bán kính: bằng nửa độ dài đường chéo hình hộp chữ nhật (hình lập phương).
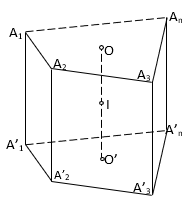
b/ Hình lăng trụ đứng có đáy nội tiếp đường tròn.
Xét hình lăng trụ đứng A1A2A3...An.A'1A'2A'3...A'n, trong đó có 2 đáy A1A2A3...An và A'1A'2A'3...A'n nội tiếp đường tròn (O) và (O'). Lúc đó, mặt cầu nội tiếp hình lăng trụ đứng có:
- Tâm: I với I là trung điểm của OO'
- Bán kính: R = IA1 = IA2 = ... = IAn
c/ Hình chóp có các đỉnh nhìn đoạn thẳng nối 2 đỉnh còn lại dưới 1 góc vuông.
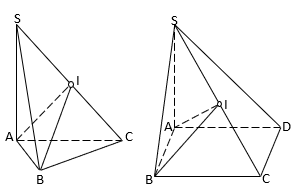
- Hình chóp S.ABC có:
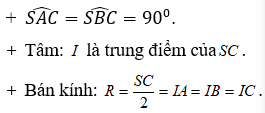
- Hình chóp S.ABCD có:
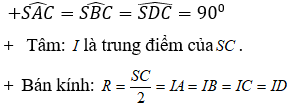
Cách xác định mặt cầu nội tiếp, ngoại tiếp hình chóp
Phương pháp giải
a. Mặt cầu ngoại tiếp hình chóp.
+ Xác định trục d của đường tròn ngoại tiếp đa giác đáy (d là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).
+ Xác định mặt phẳng trung trực (P) của một cạnh bên (hoặc trục Δ của của đường tròn ngoại tiếp một đa giác của mặt bên).
+ Giao điểm I của (P) và d (hoặc của Δ và d ) là tâm mặt cầu ngoại tiếp.
+ Kết luận: I là tâm mặt cầu ngoại tiếp chóp.
Nhận xét: Hình chóp có đáy hoặc các mặt bên là các đa giác không nội tiếp được đường tròn thì hình chóp đó không nội tiếp được mặt cầu.
b. Mặt cầu nội tiếp hình chóp.
*Điều kiện tồn tại mặt cầu nội tiếp được khối chóp: Nếu trên đáy của một hình chóp tồn tại một điểm cách đều tất cả các mặt xung quanh của hình chóp thì hình chóp đó có một hình cầu nội tiếp.
*Cách xác định tâm mặt cầu nội tiếp khối chóp có hình chiếu vuông góc của đỉnh trùng với điểm ở đáy mà cách đều tất cả các mặt bên:
- Xác định được điểm O cách đều trên đáy.
- Nối đỉnh hình chóp với O bằng một đoạn thẳng.
- Dựng mặt phẳng phân giác của một góc nhị diện nào đó ở đáy. Giao điểm của mặt phẳng phân giác với đường thẳng trên là tâm hình cầu nội tiếp cần tìm.
*Nếu đặt V là thể tích khối chóp và Stp là tổng diện tích mặt đáy và các mặt bên của chóp (diện tích toàn phần) thì bán kính r của mặt cầu ngoại tiếp khối chóp là:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho phương trình log9x2-log3(5x-1)=-log3m (Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm?
Câu 3:
Xác định a,b để hàm số y=ax-1x+b có đồ thị như hình vẽ bên. Chọn đáp án đúng?
Câu 4:
Hàm số y=ax4+bx2+c có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
Câu 5:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
Câu 6:
Cho hình nón có diện tích xung quanh bằng 3πa2 và có bán kính đáy bằng a. Độ dài đường sinh của hình nón đã cho bằng
Câu 7:
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên.
Hàm số y=f(x) có bao nhiêu điểm cực trị ?
Câu 8:
Tìm giá trị thực của tham số m để hàm số y=13x3-mx2+(m2-4)x+3 đạt cực đại tại x=3?
Câu 10:
Cho hàm số f(x) có đạo hàm . Số điểm cực trị của hàm số đã cho là
Câu 12:
Cho khối chóp có diện tích đáy và chiều cao h=2a. Thể tích khối chóp đã cho bằng
Câu 13:
Cho hàm số y=f(x) có bảng biến thiên như hình dưới
Số điểm cực trị của hàm số là
Câu 14:
Cho hàm số y=f(x) có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng?
Câu 15:
Cho hàm số f(x) có bảng biến thiên như sau:
Hàm số đồng biến trên khoảng nào?

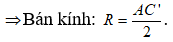
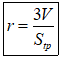


![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)