Câu hỏi:
03/11/2024 341Cho hình nón có diện tích xung quanh bằng và có bán kính đáy bằng a. Độ dài đường sinh của hình nón đã cho bằng
A. 3a
B. 2a
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A.
*Lời giải:
Ta có Thay R=a
Suy ra l=3a
*Phương pháp giải:
- Diện tích xung quanh hình nón: Sxq = πRl.
- từ đó suy ra l = ?
* Các lý thuyết thêm về mặt trụ, mặt cầu và mặt nón:
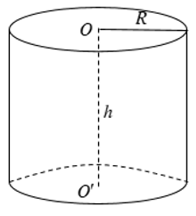
1. Diện tích và thể tích hình trụ
Cho hình trụ có bán kính đáy R và chiều cao h.
- Diện tích xung quanh: Sxq = 2πRh.
- Diện tích toàn phần: Stp = 2πRh + 2πR2.
- Thể tích: V = πR2h.
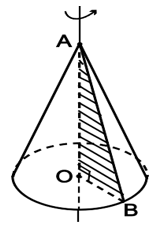
2. Diện tích và thể tích của hình nón
Đặt AC = l; l là đường sinh.
Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.
- Diện tích xung quanh: Sxq = πRl.
- Diện tích toàn phần: Stp = πRl + πR2.
- Thể tích: .
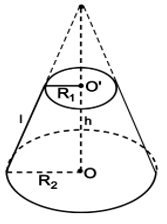
3. Diện tích và thể tích hình nón cụt
Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.
- Diện tích xung quanh: Sxq = π (R + r) l.
- Thể tích: .
Xem thêm các bài viết liên quan hay, chi tiết
Chuyên đề Mặt nón, mặt trụ, mặt cầu mới nhất - Toán 12
190 Bài trắc nghiệm Mặt nón, mặt trụ, mặt cầu cực hay có lời giải chi tiết
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB=3a, BC=4a, SA=12a và SA vuông góc với đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD
Câu 2:
Cho phương trình (Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm?
Câu 4:
Xác định a,b để hàm số có đồ thị như hình vẽ bên. Chọn đáp án đúng?
Câu 5:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
Câu 8:
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên.
Hàm số y=f(x) có bao nhiêu điểm cực trị ?
Câu 9:
Cho hàm số f(x) có đạo hàm . Số điểm cực trị của hàm số đã cho là
Câu 12:
Cho khối chóp có diện tích đáy và chiều cao h=2a. Thể tích khối chóp đã cho bằng
Câu 13:
Cho hàm số y=f(x) có bảng biến thiên như hình dưới
Số điểm cực trị của hàm số là
Câu 14:
Cho hàm số y=f(x) có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng?
Câu 15:
Cho hàm số f(x) có bảng biến thiên như sau:
Hàm số đồng biến trên khoảng nào?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)