Câu hỏi:
14/07/2024 98
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M, N lần lượt là trung điểm của AB, CD. (P) là mặt phẳng đi qua MN và song song với mặt phẳng (SAD). Tìm giao tuyến của các mặt của hình chóp với mặt phẳng (P).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M, N lần lượt là trung điểm của AB, CD. (P) là mặt phẳng đi qua MN và song song với mặt phẳng (SAD). Tìm giao tuyến của các mặt của hình chóp với mặt phẳng (P).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
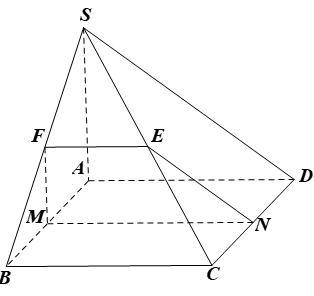
Do M, N lần lượt là trung điểm của AB, CD nên MN // BC // AD.
Mà AD ⊂ (SAD) nên MN // (SAD).
Gọi E là trung điểm của SC.
Xét ∆SCD có N, E lần lượt là trung điểm của CD, SC nên NE là đường trung bình của tam giác, suy ra NE // SD.
Mà SD ⊂ (SAD) nên NE // (SAD).
Ta có: MN // (SAD);
NE // (SAD);
MN ∩ NE = N trong (MNE).
Do đó (MNE) // (SAD).
Khi đó (MNE) chính là mặt phẳng (P).
Gọi F là trung điểm của SB, tương tự ta cũng có (MNEF) là mặt phẳng (P).
Vậy, (P) ∩ (ABCD) = MN với MN // BC // AD.
(P) ∩ (SAB) = MF với MF // SA (F là trung điểm của SB).
(P) ∩ (SDC) = NE với NE // SD (E là trung điểm của SC).
(P) ∩ (SBC) = EF.

Do M, N lần lượt là trung điểm của AB, CD nên MN // BC // AD.
Mà AD ⊂ (SAD) nên MN // (SAD).
Gọi E là trung điểm của SC.
Xét ∆SCD có N, E lần lượt là trung điểm của CD, SC nên NE là đường trung bình của tam giác, suy ra NE // SD.
Mà SD ⊂ (SAD) nên NE // (SAD).
Ta có: MN // (SAD);
NE // (SAD);
MN ∩ NE = N trong (MNE).
Do đó (MNE) // (SAD).
Khi đó (MNE) chính là mặt phẳng (P).
Gọi F là trung điểm của SB, tương tự ta cũng có (MNEF) là mặt phẳng (P).
Vậy, (P) ∩ (ABCD) = MN với MN // BC // AD.
(P) ∩ (SAB) = MF với MF // SA (F là trung điểm của SB).
(P) ∩ (SDC) = NE với NE // SD (E là trung điểm của SC).
(P) ∩ (SBC) = EF.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA và CD.
a) Chứng minh (OMN) // (SBC).
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA và CD.
a) Chứng minh (OMN) // (SBC).
Câu 2:
b) Giả sử hai tam giác SAD và SAB là các tam giác cân tại A. Gọi AE và AF lần lượt là đường phân giác trong của hai tam giác SAD và SAB. Chứng minh EF // (SBD).
b) Giả sử hai tam giác SAD và SAB là các tam giác cân tại A. Gọi AE và AF lần lượt là đường phân giác trong của hai tam giác SAD và SAB. Chứng minh EF // (SBD).
Câu 3:
c) Tìm giao điểm K của FI với giao tuyến vừa tìm được ở câu b, từ đó chứng minh (SBF) // (KCD).
c) Tìm giao điểm K của FI với giao tuyến vừa tìm được ở câu b, từ đó chứng minh (SBF) // (KCD).
Câu 4:
Cho hình chóp S.ABCD có đáy là hình thang ABCD, AD // BC, AD = 2BC. Gọi E, F, I lần lượt là trung điểm của các cạnh SA, AD, SD.
a) Chứng minh: (BEF) // (SCD) và CI // (BEF).
Cho hình chóp S.ABCD có đáy là hình thang ABCD, AD // BC, AD = 2BC. Gọi E, F, I lần lượt là trung điểm của các cạnh SA, AD, SD.
a) Chứng minh: (BEF) // (SCD) và CI // (BEF).
Câu 7:
b) Đường chéo AC’ đi qua trọng tâm G và G’ của hai tam giác BDA’ và B’D’C.
b) Đường chéo AC’ đi qua trọng tâm G và G’ của hai tam giác BDA’ và B’D’C.


