Giải SBT Toán 11 CTST Bài 4. Hai mặt phẳng song song
-
68 lượt thi
-
9 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
14/07/2024Cho hình chóp S.ABCD có đáy là hình thang ABCD, AD // BC, AD = 2BC. Gọi E, F, I lần lượt là trung điểm của các cạnh SA, AD, SD.
a) Chứng minh: (BEF) // (SCD) và CI // (BEF).
Xem đáp án
a) • Xét ∆SAD có E, F lần lượt là trung điểm của các cạnh SA, AD nên EF là đường trung bình của tam giác SAD, suy ra EF // SD.
Mà SD ⊂ (SCD), suy ra EF // (SCD).
Ta có F là trung điểm của AD nên
Mà AD = 2BC hay nên BC = AF = FD.
Lại có BC // AD hay BC // FD
Do đó tứ giác BFDC là hình bình hành nên BF // CD
Mà CD ⊂ (SCD)
Suy ra BF // (SCD).
Ta có: EF // (SCD);
BF // (SCD);
EF ∩ BF = F trong (BEF).
Suy ra (BEF) // (SCD).
• Xét ∆SAD có: E, I lần lượt là trung điểm của SA, SD
Suy ra EI là đường trung bình của ∆SAD, do đó EI // AD và
Mà AD // BC và
Suy ra EI // BC và
Do đó tứ giác EICB là hình bình hành nên CI // BE.
Mặt khác BE ⊂ (BEF), suy ra CI // (BEF).
Câu 2:
20/07/2024b) Tìm giao tuyến của hai mặt phẳng (SBC) và (SAD).
Xem đáp án
b) Ta có BC // AD, BC ⊂ (SBC) và AD ⊂ (SAD)
Suy ra giao tuyến của (SBC) và (SAD) là đường thẳng d đi qua S và d // BC // AD.
Câu 3:
11/07/2024c) Tìm giao điểm K của FI với giao tuyến vừa tìm được ở câu b, từ đó chứng minh (SBF) // (KCD).
Xem đáp án
c) Do d ⊂ (SAD) và FI ⊂ (SAD) nên trong mặt phẳng (SAD), ta có d ∩ FI = K.
Xét ∆SAD có I là trung điểm của SD, F là trung điểm của AD.
Suy ra IF là đường trung bình của ∆SAD, suy ra IF // SA hay KF // SA (1)
Mặt khác, SK // AF (2).
Từ (1) và (2) suy ra SKFA là hình bình hành, do đó SK = AF.
Suy ra SK = FD (vì AF = FD).
Tứ giác SKDF có SK = FD và SK // FD, nên SKDF là hình bình hành.
Suy ra SF // KD.
Ta có SF // KD và KD ⊂ (KCD) nên SF // (KCD).
BF // DC và DC ⊂ (KCD) nên BF // (KCD).
Lại có, trong (SBF) thì SF ∩ BF = F
Suy ra (SBF) // (KCD).
Câu 4:
23/07/2024Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA và CD.
a) Chứng minh (OMN) // (SBC).
Xem đáp án
a) • Xét ∆SAC có: M, O lần lượt là trung điểm của SA, AC nên MO là đường trung bình của tam giác SAC, suy ra MO // SC.
Mà SC ⊂ (SCB), suy ra MO // (SCB).
• Xét ∆DCB có: N, O lần lượt là trung điểm của CD, BD nên NO là đường trung bình của tam giác DCB, suy ra NO // BC
Mà BC ⊂ (SBC), suy ra NO // (SCB).
Ta có: MO // (SCB);
NO // (SCB);
MO, NO ⊂ (OMN); MO ∩ NO = O.
Vậy (OMN) // (SBC).
Câu 5:
17/07/2024b) Giả sử hai tam giác SAD và SAB là các tam giác cân tại A. Gọi AE và AF lần lượt là đường phân giác trong của hai tam giác SAD và SAB. Chứng minh EF // (SBD).
Xem đáp án
b) Ta có hai tam giác SAD và SAB là các tam giác cân tại A, suy ra AE và AF vừa là
phân giác vừa là đường trung tuyến lần lượt của hai tam giác SAD và SAB, suy ra E và F lần lượt là trung điểm của SD và SB.
Suy ra EF là đường trung bình của tam giác SDB nên EF // BD
Mà BD ⊂ (SBD)
Suy ra EF // (SBD).
Câu 6:
21/07/2024Cho hình hộp ABCD.A’B’C’D’. Chứng minh:
a) (BDA’) // (B’D’C).
Xem đáp án
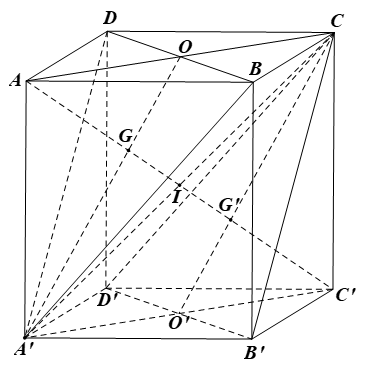
a) Ta có DD’ // BB’ và DD’ = BB’ (do ABCD.A’B’C’D’ là hình hộp), suy ra DD’B’B là hình bình hành, suy ra BD // B’D’ mà B’D’ ⊂ (B’D’C), suy ra BD // (B’D’C).
Chứng minh tương tự ta có DA’ // B’C, mà B’C ⊂ (B’D’C).
Suy ra DA’ // (B’D’C).
Ta có BD // (B’D’C);
DA’ // (B’D’C);
BD ∩ DA’ = D và BD, DA’ ⊂ (BDA’).
Suy ra (BDA’) // (B’D’C).
Câu 7:
10/07/2024b) Đường chéo AC’ đi qua trọng tâm G và G’ của hai tam giác BDA’ và B’D’C.
Xem đáp án
b) Gọi O, O’ lần lượt là tâm của hai đáy ABCD và A’B’C’D’.
Trong hình bình hành AA’C’C gọi I là giao điểm của AC’ và A’C; AC’ cắt A’O tại G1.
Trong tam giác AA’C, ta có G1 là giao điểm của hai trung tuyến AI và A’O nên G1 là trọng tâm của tam giác AA’C. Do đó
Mà G là trọng tâm của tam giác A’BD nên ta cũng có
Do đó G1 ≡ G hay ta xác định được G là giao điểm của AC’ và A’O.
Tương tự ta cũng xác định được trọng tâm G’ tam giác B’D’C là giao điểm của AC’ với CO’.
Vậy AC’ đi qua trọng tâm của hai tam giác BDA’ và B’D’C.
Câu 9:
14/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M, N lần lượt là trung điểm của AB, CD. (P) là mặt phẳng đi qua MN và song song với mặt phẳng (SAD). Tìm giao tuyến của các mặt của hình chóp với mặt phẳng (P).
Xem đáp án
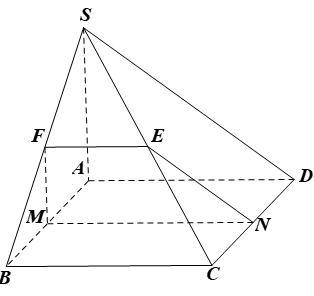
Do M, N lần lượt là trung điểm của AB, CD nên MN // BC // AD.
Mà AD ⊂ (SAD) nên MN // (SAD).
Gọi E là trung điểm của SC.
Xét ∆SCD có N, E lần lượt là trung điểm của CD, SC nên NE là đường trung bình của tam giác, suy ra NE // SD.
Mà SD ⊂ (SAD) nên NE // (SAD).
Ta có: MN // (SAD);
NE // (SAD);
MN ∩ NE = N trong (MNE).
Do đó (MNE) // (SAD).
Khi đó (MNE) chính là mặt phẳng (P).
Gọi F là trung điểm của SB, tương tự ta cũng có (MNEF) là mặt phẳng (P).
Vậy, (P) ∩ (ABCD) = MN với MN // BC // AD.
(P) ∩ (SAB) = MF với MF // SA (F là trung điểm của SB).
(P) ∩ (SDC) = NE với NE // SD (E là trung điểm của SC).
(P) ∩ (SBC) = EF.