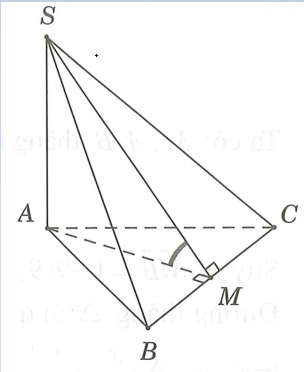
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh $a$ . Cạnh bên $SA=a\sqrt{3}$  và vuông góc với mặt đáy $\left(ABC\right)$ . Gọi  là góc giữa hai mặt phẳng $\left(SBC\right)$  và $\left(ABC\right)$ .

Mệnh đề nào sau đây đúng?

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh $a$. Cạnh bên SA vuông góc với đáy$\left(ABCD\right)$  và $SC=a\sqrt{5}$. Tính theo $a$ thể tích $V$ khối chóp S.ABCD.

Cho hai số thực dương $x,y$  thỏa mãn ${\log }_{2}x+x(x+y)\ge {\log }_2(6-y)+6x$ . Giá trị nhỏ nhất của biểu thức $P=3x+2y+\frac{6}{x}+\frac{8}{y}$  bằng

Trong không gian Oxyz, cho hai điểm $\text{A}(2;-2;4),\text{B}(-3;3;-1)$  và mặt phẳng $\left(P\right):2x-y+2z-8=0.$   Xét điểm $\text{M}$  là điểm thay đổi thuộc $\left(\text{P}\right)$ , giá trị nhỏ nhất của $2M{A}^2+3M{B}^2$  bằng

Trong không gian với hệ tọa độ $Oxyz$  cho hai mặt phẳng $\left(\alpha \right):x+y+z-1=0$  và $\left(\beta \right):2x-y+mz-m+1=\mathrm{0,}$  với $m$  là tham số thực. Giá trị của $m$  để $\left(\alpha \right)\perp \left(\beta \right)$  là

Tính $P$  là tích tất cả các nghiệm của phương trình ${3.9}^x-{10.3}^x+3=0$

Một ngôi biệt thự có 10 cây cột nhà hình trụ tròn, tất cả đều có chiều cao 4,2 m. Trong đó, 4 cây cột trước đại sảnh có đường kính $40 \text{cm}$  và 6 cây cột còn lại bên thân nhà có đường kính $26 \text{cm}$ . Chủ nhà dùng loại sơn giả đá để sơn 10 cây cột đó. Nếu giá của một loại sơn giả đá là 380.000 đồng/${\text{m}}^2$  (gồm cả tiền thi công) thì người chủ nhà phải chi bao nhiêu tiền để sơn 10 cây cột đó? (số tiền làm tròn đến hàng nghìn).

Cho điểm $M$  trên cạnh SA, điểm $N$  trên cạnh SB của hình chóp tam giác S.ABC có thể tích bằng V sao cho $\frac{SM}{SA}=\frac{1}{3},\frac{SN}{SB}=x.$  Mặt phẳng $\left(P\right)$  qua MN và song song với SC chia khối chóp S.ABC thành hai khối đa diện có thể tích bằng nhau. Khẳng định nào sau đây là đúng

Cho hàm số $y=f\left(x\right)$  liên tục trên $\left(-\infty ;1\right)$  và $\left(1;+\infty \right)$  có bảng biến thiên như sau

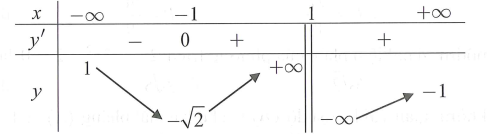
Số nghiệm thực của phương trình $2f\left(x\right)-1=0$  là

Cho hàm số $y=f\left(x\right)$  xác định trên $ℝ$  và có bảng biến thiên như hình vẽ dưới đây

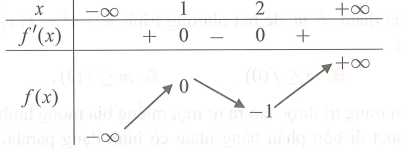
Hỏi có bao nhiêu giá trị của tham số $m$  (với  $m\in \mathbb{Z};\left|m\right|\le 2019$) để đồ thị hàm số $y=\left|m+f\left(\left|x\right|\right)\right|$  có đúng 7 điểm cực trị?

Trong không gian với hệ tọa độ$Oxyz$ , mặt phẳng $\left(P\right)$  đi qua điểm $M(3;-1;4)$ , đồng thời vuông góc với giá của vectơ $\overrightarrow{a}=(1;-1;2)$  có phương trình là

Cho hình lăng trụ $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ có đáy là tam giác đều với độ dài cạnh bằng $2a$. Hình chiếu vuông góc của $A^{\text{'}}$ lên mặt phẳng $\left(ABC\right)$ trùng với trung điểm $H$ của BC. Tính khoảng cách $d$ giữa hai đường thẳng $B{B}^{\text{'}}$ và $A^{\text{'}}H$.

Hàm số $y=x+\frac{{10}^8}{x}$  đạt giá trị nhỏ nhất trên đoạn $\left[{10}^3;{10}^9\right]$  tại $x$   bằng

Cho số phức $z={(1-2i)}^2$ . Tính mô đun của số phức $\frac{1}{z}$ .

Tìm tập hợp tất cả các giá trị của $m$  để hàm số $y=\frac{\tan x+m}{m\tan x+1}$   nghịch biến trên khoảng $\left(0;\frac{\pi }{4}\right)?$

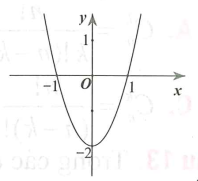
Cho hàm số $y=f\left(x\right)$  có đồ thị như hình vẽ bên.

Tìm giá trị cực đại của hàm số.