Câu hỏi:
21/07/2024 143
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo. Khẳng định nào sau đây là đúng:
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo. Khẳng định nào sau đây là đúng:
A. + = ;
A. + = ;
B. + = ;
C. − = ;
D. + = .
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
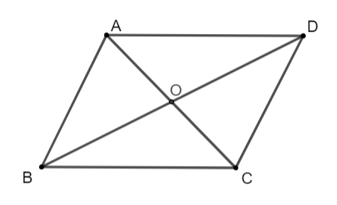
+) Vì ABCD là hình bình hành nên theo quy tắc hình bình hành ta có: + = .
Vậy đáp án A đúng.
+) Ta có: + = ≠ . Vậy đáp án B sai.
+) Ta có: − = ≠ .
Vậy đáp án C sai.
+) Vì O là giao điểm của hai đường chéo của hình bình hành nên O là trung điểm của AC, do đó, + = . Vậy đáp án D sai.
Đáp án đúng là: A
+) Vì ABCD là hình bình hành nên theo quy tắc hình bình hành ta có: + = .
Vậy đáp án A đúng.
+) Ta có: + = ≠ . Vậy đáp án B sai.
+) Ta có: − = ≠ .
Vậy đáp án C sai.
+) Vì O là giao điểm của hai đường chéo của hình bình hành nên O là trung điểm của AC, do đó, + = . Vậy đáp án D sai.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Điền vào chỗ trống: “Với ba điểm bất kì A, B, C, vectơ được gọi là … của hai vectơ và , kí hiệu là = + ”.
Điền vào chỗ trống: “Với ba điểm bất kì A, B, C, vectơ được gọi là … của hai vectơ và , kí hiệu là = + ”.
Câu 4:
Điền vào chỗ trống: “Vectơ có cùng độ dài và ngược hướng với vectơ được gọi là … của vectơ , kí hiệu là −”.
Điền vào chỗ trống: “Vectơ có cùng độ dài và ngược hướng với vectơ được gọi là … của vectơ , kí hiệu là −”.
Câu 6:
Cho hai điểm A và B phân biệt. Điều kiện để O là trung điểm AB là:
Cho hai điểm A và B phân biệt. Điều kiện để O là trung điểm AB là:


