Câu hỏi:
20/07/2024 103
Cho Hình 3.34. Biết AB // Cx, \(\widehat A = 70^\circ ;\widehat B = 60^\circ \).
Tính số đo các góc \(\widehat {{C_1}};\widehat {{C_2}};\widehat {{C_3}}\).
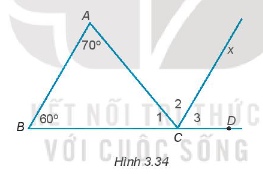
Cho Hình 3.34. Biết AB // Cx, \(\widehat A = 70^\circ ;\widehat B = 60^\circ \).
Tính số đo các góc \(\widehat {{C_1}};\widehat {{C_2}};\widehat {{C_3}}\).

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
Vì AB song song với Cx nên các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
Ta có:
\(\widehat B\) và \(\widehat {{C_3}}\) là hai góc ở vị trí đồng vị nên \(\widehat B\) = \(\widehat {{C_3}}\) = 60o;
\(\widehat A\) và \(\widehat {{C_2}}\) là hai góc ở vị trí đồng vị nên \(\widehat A\) = \(\widehat {{C_2}}\) = 70o;
Ta có: \(\widehat {{C_1}}\) + \(\widehat {{C_2}}\) + \(\widehat {{C_3}}\) = 180o.
Thay số: \(\widehat {{C_1}}\) + 70o + 60o = 180o
\(\widehat {{C_1}}\) = 180o – 60o – 70o.
\(\widehat {{C_1}}\) = 50o
Vậy \(\widehat {{C_1}}\) = 50o; \(\widehat {{C_2}}\) = 70o; \(\widehat {{C_3}}\) = 60o.
Lời giải:
Vì AB song song với Cx nên các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
Ta có:
\(\widehat B\) và \(\widehat {{C_3}}\) là hai góc ở vị trí đồng vị nên \(\widehat B\) = \(\widehat {{C_3}}\) = 60o;
\(\widehat A\) và \(\widehat {{C_2}}\) là hai góc ở vị trí đồng vị nên \(\widehat A\) = \(\widehat {{C_2}}\) = 70o;
Ta có: \(\widehat {{C_1}}\) + \(\widehat {{C_2}}\) + \(\widehat {{C_3}}\) = 180o.
Thay số: \(\widehat {{C_1}}\) + 70o + 60o = 180o
\(\widehat {{C_1}}\) = 180o – 60o – 70o.
\(\widehat {{C_1}}\) = 50o
Vậy \(\widehat {{C_1}}\) = 50o; \(\widehat {{C_2}}\) = 70o; \(\widehat {{C_3}}\) = 60o.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Hai đường thẳng AB và CD cắt nhau tại O. Cho OM là tia phân giác của góc BOD và \(\widehat {BOM} = 30^\circ \). Số đo của góc AOC bằng:
Câu 4:
Gọi Bx, Cy lần lượt là tia phân giác của các góc BE và ACF. Chứng minh rằng Bxx // Cy.
Gọi Bx, Cy lần lượt là tia phân giác của các góc BE và ACF. Chứng minh rằng Bxx // Cy.

Câu 5:
Cho Hình 3.36. Bên trong góc BOD vẽ tia Ox song song với AB. Biết \(\widehat B = 40^\circ ;\widehat D = 70^\circ ;\widehat {BOD} = 110^\circ \).
Tính số đo của góc BOx.
Cho Hình 3.36. Bên trong góc BOD vẽ tia Ox song song với AB. Biết \(\widehat B = 40^\circ ;\widehat D = 70^\circ ;\widehat {BOD} = 110^\circ \).
Tính số đo của góc BOx.
Câu 11:
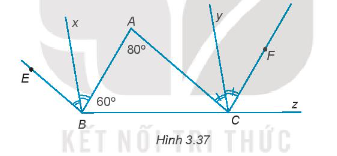
Trong Hình 3.37 có BE // AC, CF //AB. Biết \(\widehat A = 80^\circ ;\widehat {ABC} = 60^\circ \).
Chứng minh rằng \(\widehat {ABE} = \widehat {ACF}\).
Trong Hình 3.37 có BE // AC, CF //AB. Biết \(\widehat A = 80^\circ ;\widehat {ABC} = 60^\circ \).
Chứng minh rằng \(\widehat {ABE} = \widehat {ACF}\).
Câu 12:
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào trong các trường hợp sau đây?
Câu 14:
Cho Hình 3.35. Biết CN là tia phân giác của góc ACM.
Chứng minh rằng CN // AB.
Câu 15:
A. Câu hỏi (trắc nghiệm)
Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?