Giải SBT Toán 7 Ôn tập chương 3 có đáp án
Giải SBT Toán 7 Ôn tập chương 3 có đáp án
-
126 lượt thi
-
19 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
17/07/2024A. Câu hỏi (trắc nghiệm)
Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?
 Xem đáp án
Xem đáp án
Lời giải:
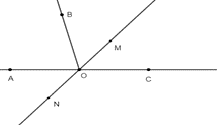
Từ hình vẽ ta thấy cặp góc đối đỉnh là ^AOM và ^CON vì OA là tia đối của tia OC và OM là tia đối của tia ON.
Đáp án đúng là C.
Câu 2:
16/07/2024 Xem đáp án
Xem đáp án
Lời giải:
Khẳng định đúng là: Hai góc đối đỉnh thì bằng nhau.
Đáp án đúng là C.
Câu 3:
16/07/2024Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Biết số đo của một trong bốn góc đó là 65o. Khi đó số đo của ba góc còn lại là:
 Xem đáp án
Xem đáp án
Lời giải:
Giả sử: đừng thẳng a cắt đường thẳng b tại O, tạo thành 4 góc ^O1;^O2;^O3;^O4 và ^O1 = 65o.
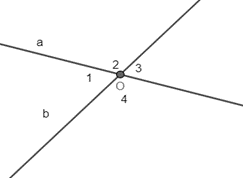
Vì ^O1 và ^O3 đối đỉnh nên ^O1 = ^O3 = 65o.
Vì ^O3 và ^O4 kề bù nên ^O3 + ^O4 = 180o.
Thay số: 65o + ^O4 = 180o
^O4 = 180o – 65o = 115o.
Mà ^O4 và ^O2 đối đỉnh nên ^O4 = ^O2 = 115o.
Vậy ^O4 = ^O2 = 115o; ^O1 = ^O3 = 65o.
Đáp án đúng là D.
Câu 4:
16/07/2024 Xem đáp án
Xem đáp án
Lời giải:
Vì hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt nên sẽ có hai cặp góc đối đỉnh.
Mà các góc đối đỉnh thì bằng nhau. Do đó, trong bốn giá trị sẽ lần lượt có hai cặp giá trị góc bằng nhau.
Nhận thấy chỉ có đáp án D thỏa mãn.
Vậy đáp án đúng là D.
Câu 5:
21/07/2024Hai đường thẳng AB và CD cắt nhau tại O. Cho OM là tia phân giác của góc BOD và ^BOM=30∘. Số đo của góc AOC bằng:
 Xem đáp án
Xem đáp án
Lời giải:
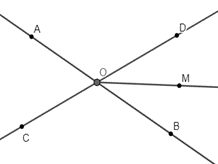
Vì OM là tia phân giác của góc BOD nên ^BOM=^MOD=^BOD2=30∘
Suy ra ^BOD = 2.30o = 60o.
Lại có, ^BOD và ^AOC là hai góc đối đỉnh nên ^BOD = ^AOC = 60o.
Đáp án đúng là B.
Câu 6:
16/07/2024Cho Hình 3.29
Cặp góc so le trong là cặp góc:
 Xem đáp án
Xem đáp án
Lời giải:
Quan sát hình vẽ ta thấy cặp góc so le trong là: ^M2;^N1.
Đáp án đúng là D.
Câu 7:
21/07/2024 Xem đáp án
Xem đáp án
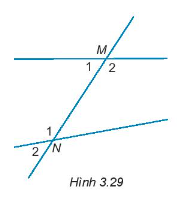
Quan sát hình vẽ ta thấy cặp góc đồng vị là: ^M1;^N2
Đáp án đúng là C.
Câu 8:
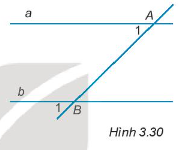
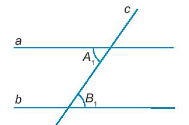
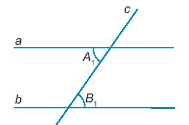
16/07/2024Cho Hình 3.30. Cặp góc A1; B1 là cặp góc:
 Xem đáp án
Xem đáp án
Lời giải:
Quan sát hình vẽ ta thấy cặp góc A1 và B1 ở vị trí đồng vị.
Đáp án đúng là C.
Câu 9:
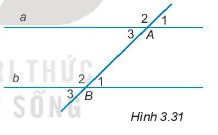
17/07/2024Cho Hình 3.31, đường thẳng a song song với đường thẳng b nếu:
 Xem đáp án
Xem đáp án
Lời giải:
Nếu có một đường thẳng cắt hai đường thẳng tạo thành các cặp góc so le trong bằng nhau hoặc các cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
Vậy để a song song với b thì các cặp góc so le trong bằng nhau hoặc các cặp góc đồng vị bằng nhau.
^A1=^B2 sai vì hai góc này không so le trong hay đồng vị;
^A2=^B3 sai vì hai góc này không so le trong hay đồng vị;
^A3=^B2sai vì hai góc này không so le trong hay đồng vị;
^A3=^B1đúng vì hai góc này ở vị trí so le trong.
Đáp án đúng là D.
Câu 10:
16/07/2024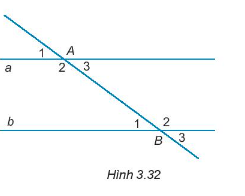
 Xem đáp án
Xem đáp án
Lời giải:
Vì a // b nên tạo ra những góc so le trong bằng nhau và những góc đồng vị bằng nhau.
^A1>^B1 sai vì hai góc này ở vị trí đồng vị nên chúng phải bằng nhau;
^A2=^B2 đúng vì hai góc này so le trong;
^A3=^B1đúng vì hai góc này so le trong;
^A3=^B3 đúng vì hai góc này đồng vị.
Câu 11:
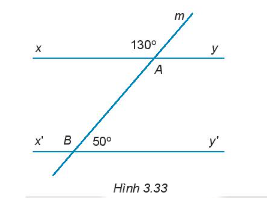
16/07/2024Cho Hình 3.33. Hãy chứng minh xy // x’y’
 Xem đáp án
Xem đáp án
Lời giải:
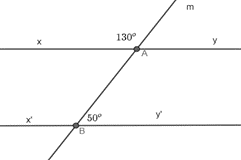
Ta có: ^mAy và ^mAx là hai góc kề bù.
Do đó, ^mAy+ ^mAy = 180o
Thay số, 130o + ^mAy = 180o.
^mAy = 180o – 130o = 50o.
Lại có, ^mAy và ^ABy′ là hai góc kề bù và ^mAy = ^ABy′ = 50o.
Do đo, xy // x’y’.
Câu 12:
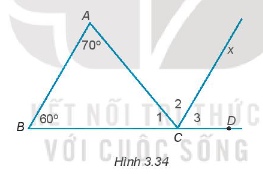
21/07/2024Cho Hình 3.34. Biết AB // Cx, ˆA=70∘;ˆB=60∘.
Tính số đo các góc ^C1;^C2;^C3.
 Xem đáp án
Xem đáp án
Lời giải:
Vì AB song song với Cx nên các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
Ta có:
ˆB và ^C3 là hai góc ở vị trí đồng vị nên ˆB = ^C3 = 60o;
ˆA và ^C2 là hai góc ở vị trí đồng vị nên ˆA = ^C2 = 70o;
Ta có: ^C1 + ^C2 + ^C3 = 180o.
Thay số: ^C1 + 70o + 60o = 180o
^C1 = 180o – 60o – 70o.
^C1 = 50o
Vậy ^C1 = 50o; ^C2 = 70o; ^C3 = 60o.
Câu 13:
16/07/2024Chứng minh rằng CN // AB.
 Xem đáp án
Xem đáp án
Lời giải:
Ta có: ^ACB và ^ACM là hai góc kề bù nên ^ACB + ^ACM = 180o.
Thay số, 40o + ^ACM = 180o
^ACM = 180o – 40o
^ACM = 140o
Vì CN là tia pân giác của góc ^ACM nên ^ACN=^NCM=^ACM2=140∘2=70∘
Ta có: ^NCM và ˆB ở vị trí đồng vị và ^NCM = ˆB = 70o.
Do đó, AB song song CN.
Câu 14:
20/07/2024 Xem đáp án
Xem đáp án
Vì AB song song với CN nên các cặp góc so le trong sẽ bằng nhau và các cặp góc đồng vị sẽ bằng nhau.
Ta có: ˆA và ^ACN là hai góc so le trong. Do đó, ^ACN = ˆA = 70o.
Vậy ˆA = 70o.
Câu 15:
16/07/2024Cho Hình 3.36. Bên trong góc BOD vẽ tia Ox song song với AB. Biết ˆB=40∘;ˆD=70∘;^BOD=110∘.
Tính số đo của góc BOx.
 Xem đáp án
Xem đáp án
Lời giải:
Vì Ox song song với AB nên các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
Ta có: ˆB và ^BOx là hai góc so le trong. Do đó, ˆB = ^BOx = 40o.
Vậy ^BOx = 40o.
Câu 16:
23/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có: ^BOD=^BOx+^xOD
Thay số, 110o = 40o + ^xOD
^xOD = 110o – 40o
^xOD = 70o
Ta có: ^xOD=^ODC = 70o mà hai góc này ở vị trí so le trong nên Ox // CD.
Lại có Ox // AB nên AB //CD (điều phải chứng minh).
Câu 17:
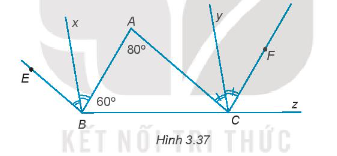
18/07/2024Trong Hình 3.37 có BE // AC, CF //AB. Biết ˆA=80∘;^ABC=60∘.
Chứng minh rằng ^ABE=^ACF.
 Xem đáp án
Xem đáp án
Lời giải:
Vì BE song song với AC nên các góc so le trong bằng nhau.
Do đó, ^ABE=ˆA=80∘ (hai góc so le trong) (1)
Vì CF song song với AB nên các góc so le trong bằng nhau.
Do đó, ^ACF=ˆA=80∘ (hai góc so le trong) (2)
Từ (1) và (2) suy ra ^ABE=^ACF = 80o.
Câu 18:
23/07/2024Tính số đo của các góc BCF và ACB.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì CF song song với AB nên các góc đồng vị bằng nhau.
Do đó, ^ABC = ^FCz (hai góc đồng vị)
Do đó, ^ABC = ^FCz = 60o.
Ta có, ^BCF và ^FCz là hai góc kề bù nên ^BCF + ^FCz = 180o.
Thay số , ^BCF + 60o = 180o
^BCF = 180o – 60o
^BCF = 120o.
Ta có:
^BCF = ^ACF+ ^ACB
120o = 80o + ^ACB
^ACB = 120o – 80o
^ACB = 40o.
Vậy ^ACB = 40o; ^BCF = 120o.
Câu 19:
22/07/2024Gọi Bx, Cy lần lượt là tia phân giác của các góc BE và ACF. Chứng minh rằng Bxx // Cy.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì Bx là tia phân giác của góc ^ABE nên ^EBx=^xBA=^EBA2=80∘2=40∘
Vì Cy là tia phân giác của góc ^ACF nên ^ACy=^yCF=^ACF2=80∘2=40∘
Ta có BC cắt Bx và cắt Cy tạo ra cặp góc đồng vị là ^zCy và ^zBx.
Ta có:
^zCy = ^yCF+ ^FCz = 40o + 60o = 100o.
^zBx= ^xBA+ ^ABC = 40o + 60o = 100o.
Suy ra, ^zCy = ^zBx= 100o
Vì ^zCy và ^zBx là hai góc đồng vị và ^zCy = ^zBx nên Bx // Cy.
