Câu hỏi:
19/07/2024 129
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x - y - 1 \ge 0\\4x - 3y - 2 \le 0\end{array} \right.\) . Miền nghiệm (miền không gạch chéo) của hệ bất phương trình được biểu diễn như trong hình vẽ nào sau đây?
A.
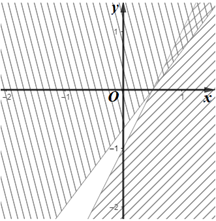

B.
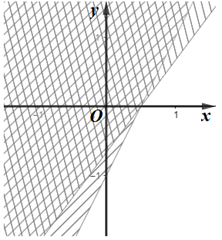

C.
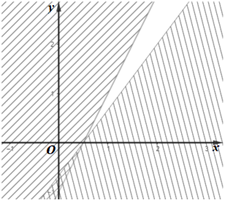

D.
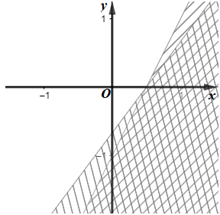

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Trên mặt phẳng Oxy:
• Biểu diễn miền nghiệm của bất phương trình: 2x – y – 1 ≥ 0.
Vẽ đường thẳng d1: 2x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 1).
Xét điểm O(0; 0) ∉ d1, ta có: 2.0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình 2x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d1) không chứa điểm O(0; 0).
• Biểu diễn miền nghiệm của bất phương trình: 4x – 3y – 2 ≤ 0.
Vẽ đường thẳng d2: 4x – 3y – 2 = 0 đi qua hai điểm (2; 2) và (–1; –2).
Xét điểm O(0; 0) ∉ d2, ta có: 4.0 – 3.0 – 2 = –2 < 0 nên miền nghiệm của bất phương trình 4x – 3y – 2 ≤ 0 là nửa mặt phẳng (kể cả bờ d2) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1 và d2) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
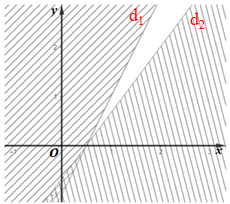
Vậy ta chọn phương án C.
Hướng dẫn giải
Đáp án đúng là: C
Trên mặt phẳng Oxy:
• Biểu diễn miền nghiệm của bất phương trình: 2x – y – 1 ≥ 0.
Vẽ đường thẳng d1: 2x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 1).
Xét điểm O(0; 0) ∉ d1, ta có: 2.0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình 2x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d1) không chứa điểm O(0; 0).
• Biểu diễn miền nghiệm của bất phương trình: 4x – 3y – 2 ≤ 0.
Vẽ đường thẳng d2: 4x – 3y – 2 = 0 đi qua hai điểm (2; 2) và (–1; –2).
Xét điểm O(0; 0) ∉ d2, ta có: 4.0 – 3.0 – 2 = –2 < 0 nên miền nghiệm của bất phương trình 4x – 3y – 2 ≤ 0 là nửa mặt phẳng (kể cả bờ d2) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1 và d2) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

Vậy ta chọn phương án C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Phần không tô đậm (không kể đường thẳng d) trong hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào?
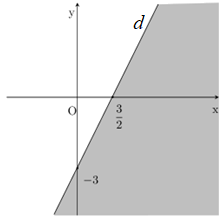
Câu 2:
Miền nghiệm của bất phương trình 3x – 2y < –6 được biểu diễn bởi miền không tô đậm trong hình vẽ nào dưới đây:
Câu 3:
Cho các đường thẳng d1: 3x – 4y + 12 = 0, d2: x + y – 5 = 0 và d3: x + 1 = 0.
Miền không gạch chéo (kể cả bờ d1, d2, d3) trong hình vẽ bên dưới là miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình dưới đây?
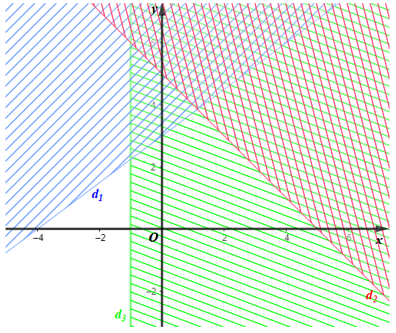
Câu 4:
Một người thợ mộc tốn 6 giờ để làm một cái bàn và 4 giờ để làm một cái ghế. Gọi x, y lần lượt là số bàn và số ghế mà người thợ mộc sản xuất trong một tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y biết trong một tuần người thợ mộc có thể làm tối đa 50 giờ.
Câu 5:
Miền nghiệm của bất phương trình 4(x – 1) + 5(y – 3) > 2x – 9 là nửa mặt phẳng chứa điểm:
Câu 6:
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - 2y < 0\\m{x^2} + 3y > 0\\2x - \left( {{m^2} - m} \right){y^2} \le 0\end{array} \right.\) (với m là tham số). Giá trị m để hệ bất phương trình đó là hệ bất phương trình bậc nhất hai ẩn x và y là:
Câu 7:
Cho hệ bất phương trình \(\left\{ \begin{array}{l}3x + 2y < 1\,\,\,\,\,\,\,\,\left( 1 \right)\\x + \frac{2}{3}y < 1\,\,\,\,\left( 2 \right)\end{array} \right..\) Gọi S1 là miền nghiệm của bất phương trình (1), S2 là miền nghiệm của bất phương trình (2).
Cho các phát biểu sau:
(I) Miền nghiệm của hệ bất phương trình là S1;
(II) Miền nghiệm của hệ bất phương trình là S2;
(III) Hai bất phương trình của hệ có cùng miền nghiệm.
Số phát biểu đúng là:


