Câu hỏi:
18/07/2024 146Cho hàm số y=x4−3x2+m có đồ thị là (Cm) với m là số thực. Giả sử (Cm) cắt trục Ox tại bốn điểm phân biệt như hình vẽ.
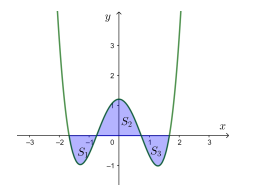
Gọi S1,S2,S3 lần lượt là diện tích các miền gạch chéo được cho như hình vẽ. Biết rằng tồn tại duy nhất giá trị m=ab với a, b là các số nguyên dương và ab tối giản sao cho S1+S3=S2. Đặt T = a + b. Mệnh đề nào đúng?
A. T∈(8;10)
B. T∈(10;13)
C. T∈(4;6)
D. T∈(6;8)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Xét phương trình hoành độ giao điểm x4−3x2+m=0 (1).
Đặt t=x2 ta có t2−3t+m=0 (2).
Vì phương trình (1) có 4 nghiệm phân biệt nên phương trình (2) có 2 nghiệm dương phân biệt
⇒{Δ=9−4m>0S=3>0P=m>0⇔0<m<94.
Giả sử t1<t2 là 2 nghiệm phân biệt của phương trình (2) thì phương trình (1) có 4 nghiệm phân biệt −√t2<−√t1<√t1<√t2.
Do tính đối xứng nên ta dễ có
S1=S3=√t2∫√t1(−x4+3x2−m)dx
=(−x55+x3−mx)|√t2√t1
=−15(t22√t2−t21√t1)+(t2√t2−t1√t1)−m(√t2−√t1)
S2=√t1∫−√t1(x4−3x2+m)dx=(x55−x3+mx)|√t1−√t1
=2(t21√t15−t1√t1+m√t1)
Theo bài ra ta có: S1+S3=2S2
⇔−15(t22√t2−t21√t1)+(t2√t2−t1√t1)−m(√t2−√t1)=t21√t15−t1√t1+m√t1
⇔−15t22√t2+t2√t2−m√t2=0
⇔√t2(−15t22+t2−m)=0
⇔−15t22+t2−m=0 (3) (do t2>0)
Vì t2 là nghiệm của phương trình (2) nên t22−3t2+m=0⇔m=−t22+3t2.
Thay vào (3) ta có:
−15t22+t2+t22−3t2=0
⇔45t22−2t2=0
⇔[t2=0(ktm)t2=52(tm)
Khi đó m=−t22+3t2=−(52)2+3.52=54(tm)⇒a=5,b=4.
Vậy T=a+b=5+4=9∈(8;10).
Chọn A.
Xét phương trình hoành độ giao điểm x4−3x2+m=0 (1).
Đặt t=x2 ta có t2−3t+m=0 (2).
Vì phương trình (1) có 4 nghiệm phân biệt nên phương trình (2) có 2 nghiệm dương phân biệt
⇒{Δ=9−4m>0S=3>0P=m>0⇔0<m<94.
Giả sử t1<t2 là 2 nghiệm phân biệt của phương trình (2) thì phương trình (1) có 4 nghiệm phân biệt −√t2<−√t1<√t1<√t2.
Do tính đối xứng nên ta dễ có
S1=S3=√t2∫√t1(−x4+3x2−m)dx
=(−x55+x3−mx)|√t2√t1
=−15(t22√t2−t21√t1)+(t2√t2−t1√t1)−m(√t2−√t1)
S2=√t1∫−√t1(x4−3x2+m)dx=(x55−x3+mx)|√t1−√t1
=2(t21√t15−t1√t1+m√t1)
Theo bài ra ta có: S1+S3=2S2
⇔−15(t22√t2−t21√t1)+(t2√t2−t1√t1)−m(√t2−√t1)=t21√t15−t1√t1+m√t1
⇔−15t22√t2+t2√t2−m√t2=0
⇔√t2(−15t22+t2−m)=0
⇔−15t22+t2−m=0 (3) (do t2>0)
Vì t2 là nghiệm của phương trình (2) nên t22−3t2+m=0⇔m=−t22+3t2.
Thay vào (3) ta có:
−15t22+t2+t22−3t2=0
⇔45t22−2t2=0
⇔[t2=0(ktm)t2=52(tm)
Khi đó m=−t22+3t2=−(52)2+3.52=54(tm)⇒a=5,b=4.
Vậy T=a+b=5+4=9∈(8;10).
Chọn A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Trong không gian Oxyz, vectơ nào là vectơ chỉ phương của đường thẳng d:x2=y+1−3=z1.
Trong không gian Oxyz, vectơ nào là vectơ chỉ phương của đường thẳng d:x2=y+1−3=z1.
Câu 6:
Từ các chữ số 1, 2, 4, 6, 8, 9 lấy ngẫu nhiên một số. Xác suất để lấy được một số chia hết cho 3 là:
Từ các chữ số 1, 2, 4, 6, 8, 9 lấy ngẫu nhiên một số. Xác suất để lấy được một số chia hết cho 3 là:
Câu 7:
Trong không gian Oxyz, điểm nào dưới đây là hình chiếu vuông góc của điểm A(3; 4; 1) trên mặt phẳng (Oxy)?
Trong không gian Oxyz, điểm nào dưới đây là hình chiếu vuông góc của điểm A(3; 4; 1) trên mặt phẳng (Oxy)?
Câu 8:
Gọi E là tập hợp tất cả các số nguyên dương y sao cho với mỗi số y có không quá 4031 số nguyên x thỏa mãn log22x−3ylog2x+2y2<0. Tập E có bao nhiêu phần tử?
Gọi E là tập hợp tất cả các số nguyên dương y sao cho với mỗi số y có không quá 4031 số nguyên x thỏa mãn log22x−3ylog2x+2y2<0. Tập E có bao nhiêu phần tử?
Câu 9:
Trong không gian Oxyz tìm tất cả các giá trị của tham số m để phương trình x2+y2+z2−2z−2y−4z+m=0 là phương trình của một mặt cầu.
Câu 10:
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x2+y2+z2=25. Từ điểm A thay đổi trên đường thẳng (Δ):{x=10+ty=−tz=10+t, kẻ các tiếp tuyến AB, AC, AD tới mặt cầu (S) với B, C, D là các tiếp điểm. Biết mặt phẳng (BCD) luôn chứa một đường thẳng cố định. Góc giữa đường thẳng cố định với mặt phẳng (Oxy) bằng:
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x2+y2+z2=25. Từ điểm A thay đổi trên đường thẳng (Δ):{x=10+ty=−tz=10+t, kẻ các tiếp tuyến AB, AC, AD tới mặt cầu (S) với B, C, D là các tiếp điểm. Biết mặt phẳng (BCD) luôn chứa một đường thẳng cố định. Góc giữa đường thẳng cố định với mặt phẳng (Oxy) bằng:
Câu 11:
Cho cấp số nhân (un) có u1=2 và công bội q = 3. Giá trị u2 bằng:
Câu 12:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SC với mặt phẳng (SAB) bằng 300. Thể tích của khối chóp S.ABCD bằng:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SC với mặt phẳng (SAB) bằng 300. Thể tích của khối chóp S.ABCD bằng:
Câu 13:
Cho biết 1∫0x3ln(4−x24+x2)dx=a+blnpq với p, q là các số nguyên tố và p > q. Tính S=2ab+pq.
Cho biết 1∫0x3ln(4−x24+x2)dx=a+blnpq với p, q là các số nguyên tố và p > q. Tính S=2ab+pq.
Câu 14:
Có một cốc thủy tính hình trụ, bán kính trong lòng cốc là 4cm, chiều cao trong lòng cốc là 10cm đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết khi nghiệm cốc nước vừa lúc chạm miệng cốc thì ở đáy mực nước trùng với đường kính đáy.
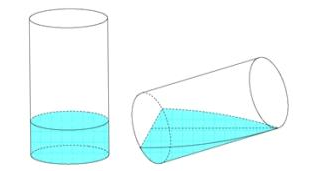
Có một cốc thủy tính hình trụ, bán kính trong lòng cốc là 4cm, chiều cao trong lòng cốc là 10cm đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết khi nghiệm cốc nước vừa lúc chạm miệng cốc thì ở đáy mực nước trùng với đường kính đáy.




![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)