Câu hỏi:
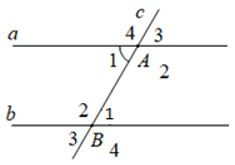
18/07/2024 333Cho định lí : "Hai tia phân giác của hai góc kề bù tạo thành một góc vuông" (hình vẽ). Giả thiết, kết luận của định lí là:
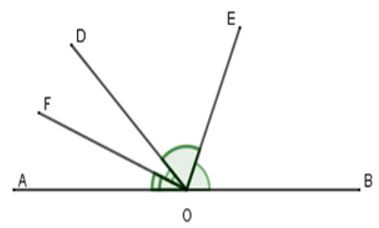
A. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.
Kết luận: OE⊥OF
B. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOF; OF là phân giác góc AOD.
Kết luận: OE⊥OA
C. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOE.
Kết luận: OE⊥OF
D. Giả thiết: Cho góc bẹt AOBAOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AODAOD.
Kết luận: OB⊥OF
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: C
Giải thích:
Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.
Kết luận: OE⊥OF
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho định lý: “Hai góc cùng phụ với một góc thứ ba thì bằng nhau”. Hãy điền từ thích hợp vào chỗ trống để hoàn tất chứng minh định lý
- Ta có: (do hai góc kề bù)
- Ta lại có: ( do hai góc kề bù)
Từ (1) và (2) suy ra:
Câu 2:
Cho định lý: Đường trung bình của tam giác thì song song với cạnh đáy và bằng một nửa cạnh đáy. Sắp xếp các bước sau để hoàn thành chứng minh định lý:
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC. Chứng minh MN //BC, . Ta thực hiện các bước sau:
1) Từ (1) và (2) suy ra MN//BC và .
2) Xét và , ta có:
AN = NC ( N là trung điểm AC )
(hai góc đối đỉnh)
MN = NP ( N là trung điểm của MP)
(2 cạnh tương ứng)
Mà AM = MB (M là trung điểm của AB)
.
3) Trên tia đối của NM lấy điểm P sao cho N là trung điểm của MP.
4) Xét và , ta có:
BP: chung
(cmt)
MB = CP (cmt)
(hai góc tương ứng)
Mà hai góc ở vị trí so le trong
hay MN//BC (1)
5) Vì (cmt)
(hai góc tương ứng)
Mà hai góc ở vị trí so le trong
(hai góc so le trong)
6) Vì
(2 cạnh tương ứng)
Mà (do N là trung điểm của MP)
(2)
Câu 4:
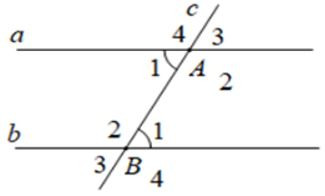
Định lí: "Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau" (như hình vẽ dưới đây). Giả thiết của định lí là:
Câu 10:
Phần giả thiết: (tham khảo hình vẽ) là của định lý nào dưới đây?